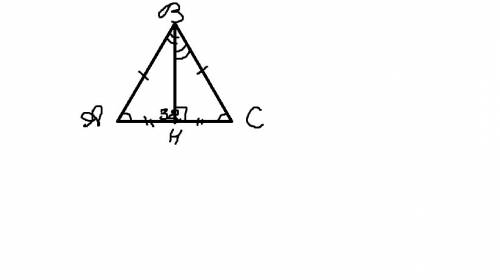
Дано:
АBC - равнобедренный треугольник.
АС=32
АВ=ВС(боковые стороны)
tg A = 5/4
s-?
Проведем высоту BH. Т.к. треугольник равнобедренный, то она также биссектриса и медиана. Получим 2 прямоугольных треугольника ABH и HBC.
tg A=BH/AH(отношение противолежащего катета к прилежащему)
Т.к. BH медиана, АН=32/2=16
По условию tg A=5/4, значит BH и АН можно представить как 5х и 4х соответственно.
АН=16=4х, х=4
ВН=5х=5*4=20
Площадь треугольника равна половине произведения основания на высоту:
Основание АС=32, Высота - 20.
Следовательно s=(32*20)/2=320
ответ:320
в точке 0;0 уравнение будет вида
0=|0+а|+б
в точке 1;1/4
1/4=|2+а|+б
подставляем значение б из первого
1/4=|2+а|-|а|
в случае, если а>0, уравнение решений не имеет:
1/4=2+а-а
в случае если -2<а<0
1/4=2+а+а
2а=-7/4
а=-7/8, б=-7/8
в случае а<-2,
1/4=-2-а+а, что тоже решений не имеет, получается единственное решение
а=-7/8, б=-7/8