Объяснение:
Удаляем знак модуля и превращаем в квадратное уравнение: y =2*x²- 9*x- 5 ≥ 0 - квадратное уравнение.
D = b² - 4*a*c = (-9)² - 4*(2)*(-5) = 121 - дискриминант. √D = 11.
x₁ = (-b+√D)/(2*a) = (9+11)/(2*2) = 20/4 = 5 - первый корень
x₂ = (-b-√D)/(2*a) = (9-11)/(2*2) = -2/4 = -0,5 - второй корень
Это две точки где границы уравнения задачи. Записываем неравенство:
y ≥ 20 при х ∈(-∞;- 0.5]∪[5;+∞)
Наименьшее положительное - х = 5 - ответ.
Рисунок с графиком функции показывает, что отрицательным это выражение не бывает.
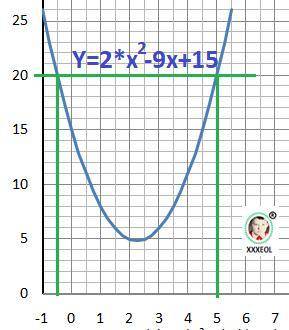
Объяснение:
Удаляем знак модуля и превращаем в квадратное уравнение: y =2*x²- 9*x- 5 ≥ 0 - квадратное уравнение.
D = b² - 4*a*c = (-9)² - 4*(2)*(-5) = 121 - дискриминант. √D = 11.
x₁ = (-b+√D)/(2*a) = (9+11)/(2*2) = 20/4 = 5 - первый корень
x₂ = (-b-√D)/(2*a) = (9-11)/(2*2) = -2/4 = -0,5 - второй корень
Это две точки где границы уравнения задачи. Записываем неравенство:
y ≥ 20 при х ∈(-∞;- 0.5]∪[5;+∞)
Наименьшее положительное - х = 5 - ответ.
Рисунок с графиком функции показывает, что отрицательным это выражение не бывает.

1)(а+b)(6+a+b)
2)( c-3)^2+(c+3)(c-3)=(c-3)(c-3+c+3)=(c-3)×c
3)8a (x+2y)-3b (x+2y)=(x+2y)(8a-3b)
вычислить:
287-287×48+239×713=287 (1-48)+239=287×(-47)+239=-13489+239=-13250
упростить :
0,01a^2-0,04a+0,04b^2+0,01a^2-0,04b^2=0,02a^2+0,04b^2=0,02×(-50)^2+0,04×(-4)^2=50+0,64=50,64
где b=-4,a=-50