Вкладчик положил в банк некоторую сумму денег из счёта 7% годовых. через год он снял со своего вклада 600 рублей , в результате чего на его счет осталась сумма , равна половине первоначального вклада. какая сумма денег будет на счету у вкладчика в конце второго года хранения ? (ответ округляй до целого числа на каждом этапе решения)

👇

Ответ:

Shnella

10.02.2021

Пусть первоначальная сумма вклада равна х руб.,
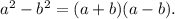
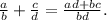
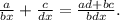
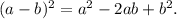
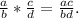
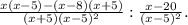
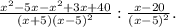
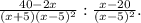
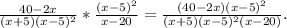
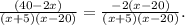
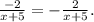
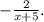
тогда ровно через 1 год на счёте будет 1,07*х руб.
После того, как вкладчик снимет со счёта 600 руб., у него на счёте останется половина суммы первоначального вклада, т.е. 0,5*х руб.
Составляем уравнение:
1,07*х-600=0,5*х
1,07*х -0,5*х =600
0,57*х =600
х=600:0,57
х=1052,63...≈1053 (руб.) - сумма первоначального вклада
1053*0,5=526,5≈527(руб.) - сумма в конце 1 года после снятия 600 руб.
527*1,07=563,89≈564(руб.) - на счёте в конце второго года хранения

4,4(55 оценок)

Открыть все ответы

Ответ:

bulycheva0303

10.02.2021

Это "почти" одно и то же...
степенная функция --это один из случаев функции в общем виде:
у = х (в степени (n/m)) и,
если вдруг окажется (m) числом четным, а (х) числом отрицательным, то мы получим корень четной степени из отрицательного числа, а это невозможно...
потому, чтобы описать свойства вообще всех функций вида:
у = х (в степени (n/m)) полагают, что х > 0
даже =0 не рассматриваем, т.к. если показатель степени отрицательный, то все выражение попадает в знаменатель и не может быть =0
а вот кубический корень --это точно в числителе (из нуля извлекается) и из отрицательного числа тоже извлекается --ограничений никаких нет...
т.е. функция "корень кубический" -это очень похоже на конкретный частный случай более общего понятия --"степенной функции с дробно рациональным показателем степени"))) это другая функция, показатель степени точно нечетное число, знаменателя нет...
например, для функции у = 1 / ∛х тоже ведь наступают ограничения...
потому для определенности говорим: ∛(-8) = -2 (существует),
а вот (-8)^(1/3) не определено, т.к. -8<0 --это другая функция, степенная с дробным показателем и показатель степени может быть любым...
(например, 1/4)))

4,6(34 оценок)

Ответ:

privetikivsem

10.02.2021

Начнем с того, что я выпишу все формулы, которые я буду использовать здесь.
1. Разность квадратов.
a^2-b^2=(a+b)(a-b).

2. Приведение дробей к общему знаменателю.
$\frac{a}{b}+ \frac{c}{d}= \frac{ad+bc}{bd}.$
Причем, если знаменатели имеют общий множитель, то на него можно и не домножать. Как к примеру тут: $\frac{a}{bx}+ \frac{c}{dx}= \frac{ad+bc}{bdx}.$
3. Квадрат разности.
(a-b)^2=a^2-2ab+b^2.

4. Умножение дробей.
$\frac{a}{b}* \frac{c}{d}= \frac{ac}{bd}.$
(Числитель умножаем с числителем, а знаменатель - со знаменателем.)
5. Деление дробей.
$\frac{a}{b}: \frac{c}{d}= \frac{a}{b}* \frac{d}{c}= \frac{ad}{bc}.$
(Вторую дробь (делитель) переворачиваем, а знак деления заменяем умножением.)
6. Умножение многочлена на многочлен.
Чтобы умножить два многочлена между собой, надо каждый член первого многочлена умножить на каждый член второго многочлена.
(a+b)(c+d)=ac+ad+bc+bd.

1). Преобразуем немного наше выражение.
$( \frac{x}{x^2-5^2}- \frac{x-8}{x^2-2*5*x+5^2}): \frac{x-20}{(x-5)^2} .$
2). Видно, что в знаменателе первой дроби можно использовать формулу разности квадратов, а в знаменателе второй дроби полный квадрат (квадрат разности). Применим эти формулы.
$(\frac{x}{(x-5)(x+5)}- \frac{x-8}{(x-5)^2}): \frac{x-20}{(x-5)^2}.$
3). Приведем первые две дроби общему знаменателю.
$\frac{x(x-5)-(x-8)(x+5)}{(x+5)(x-5)^2} : \frac{x-20}{(x-5)^2}.
$
4). Раскрываем скобки в числителе первой дроби.
$\frac{x^2-5x-x^2+3x+40}{(x+5)(x-5)^2} : \frac{x-20}{(x-5)^2}.$
5). Приводим подобные слагаемые.
$\frac{40-2x}{(x+5)(x-5)^2} : \frac{x-20}{(x-5)^2}.$
6). Делим, а затем умножаем дроби.
$\frac{40-2x}{(x+5)(x-5)^2} * \frac{(x-5)^2}{x-20}= \frac{(40-2x)(x-5)^2}{(x+5)(x-5)^2(x-20)} .$
7). Сокращаем дроби и выносим общий множитель (-2) в числителе.
$\frac{(40-2x)}{(x+5)(x-20)}= \frac{-2(x-20)}{(x+5)(x-20)} .$
8). Опять сокращаем.
$\frac{-2}{x+5}=- \frac{2}{x+5} .$
ответ: $- \frac{2}{x+5}.$