ответ:решение ниже
Объяснение:
пусть меньшая сторона площадки a= x, тогда бОльшая сторона равна b=(x+2)
площадь  =x*(x+2)=120 м.кв
=x*(x+2)=120 м.кв
откроем скобки и решим квадратное уравнение
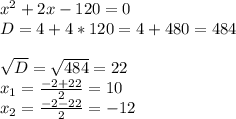
корень равный -12 не подходит поскольку размер не может быть отрицательным значением.
Получаем что:
сторона площадки а = 10 м - меньшая
сторона площадки b=10+2=12 м - бОльшая
сумма длин всех сторон площадки даст ответ на вопрос сколько необходимо бордюра, сумма длин всех сторон есть периметр
P=a+b+a+b=10+12+10+12=44 м
Если в одной упаковке 8 метров материала, то чтобы посчитать количество упаковок, необходимо требуемую длину разделить на объем упаковки:
44/8=5, 5 упаковок.
т.е. для построения бордюра потребуетсz 6 упаковок
ответ:решение ниже
Объяснение:
пусть меньшая сторона площадки a= x, тогда бОльшая сторона равна b=(x+2)
площадь  =x*(x+2)=120 м.кв
=x*(x+2)=120 м.кв
откроем скобки и решим квадратное уравнение
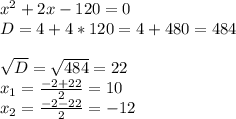
корень равный -12 не подходит поскольку размер не может быть отрицательным значением.
Получаем что:
сторона площадки а = 10 м - меньшая
сторона площадки b=10+2=12 м - бОльшая
сумма длин всех сторон площадки даст ответ на вопрос сколько необходимо бордюра, сумма длин всех сторон есть периметр
P=a+b+a+b=10+12+10+12=44 м
Если в одной упаковке 8 метров материала, то чтобы посчитать количество упаковок, необходимо требуемую длину разделить на объем упаковки:
44/8=5, 5 упаковок.
т.е. для построения бордюра потребуетсz 6 упаковок
sin x=2tg (x/2) /(1+tg^2 (x/2));
cosx=(1-tg^2 (x/2)) /(1+tg^2 (x/2))
28*(1-tg^2 (x/2)) /(1+tg^2 (x/2)) - 3*2tg(x/2) /(1+tg^2 (x/2) -8=0
1+tg^2 (x/2)≠0; 28*(1-tg^2 (x/2)) -6tg(x/2)-8*(1+tg^2 (x/2))=0
28 - 28tg^2 (x/2) - 6tg(x/2)-8 - 8tg^2 (x/2)=0
-36tg^2 (x/2)-6tg (x/2)+20=0
18tg^2 (x/2)+3tg(x/2)-10=0
tg(x/2)=t; 18t^2 +3t-10=0; D=9-4*18*(-10)=9+720=729=27^2;
t1=(-3-27)/36=-30/36=-5/6; t2=24/36=4/6=2/3
tg(x/2)=-5/6 ili tg(x/2)=2/3
x/2=-arctg(5/6)+πn x=2*arctg(2/3)+2*πn; n-celoe
x=-2arctg(5/6)+2πn