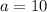(a²+4)/(4a)
Объяснение:
Как бестолково написано: (2-a/2+a-a+2/a-2):(2+a/2-a+a-2/a+2).
Может всё-таки так?
((2-a)/(2+a) -(a+2)/(a-2))÷((2+a)/(2-a) +(a-2)/(a+2))=(a²+4)/(4a)
1) (2-a)/(2+a) -(a+2)/(a-2)=(2-a)/(2+a) +(a+2)/(2-a)=((a-2)²+(a+2)²)/(4-a²)
2)(2+a)/(2-a) +(a-2)/(a+2)=(a-2)/(a+2) -(2+a)/(a-2)=((a-2)²-(a+2)²)/(a²-4)
3) ((a-2)²+(a+2)²)/(4-a²) ÷((a-2)²-(a+2)²)/(a²-4)=-((a-2)²+(a+2)²)/(a²-4) ·(a²-4)/((a-2)²-(a+2)²)=-(a²-4a+4+a²+4a+4)/((a-2-a-2)(a-2+a+2))=-(2a²+8)/(-4·2a)=(-2(a²+4))/(-4·2a)=(a²+4)/(4a)
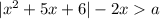
Анализируем: решение квадратного неравенства только вида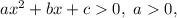 
может содержать промежуток 
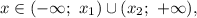где 
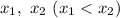— корни квадратного уравнения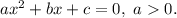 
Раскроем модуль. Для этого воспользуемся правилом: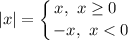 
1) Пусть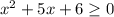 
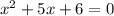
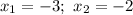— абсциссы точек пересечения с осью абсцисс.
![x \in (-\infty; \ -3] \cup [-2; \ +\infty)](/tpl/images/1106/1316/ec0c2.png)
Тогда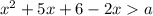 
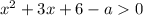
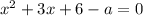
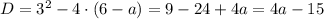
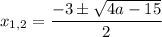
Решением исходного неравенства будет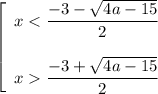 
Следовательно, зная интервал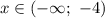 
, определим значение параметра 
:
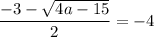
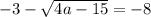
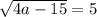
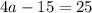
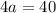
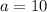
Таким образом,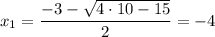 
и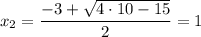 
Решение: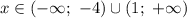 
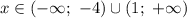При пересечении условия модуля получаем окончательное решение: при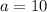
2) Если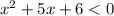 
, то получаем 
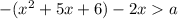с отрицательным коэффициентом перед 
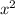: это означает, что решением квадратного неравенства вида 
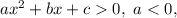будет промежуток 
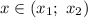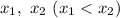, где — корни квадратного уравнения 
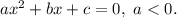Этот случай нас не устраивает.
ответ: 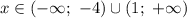при
