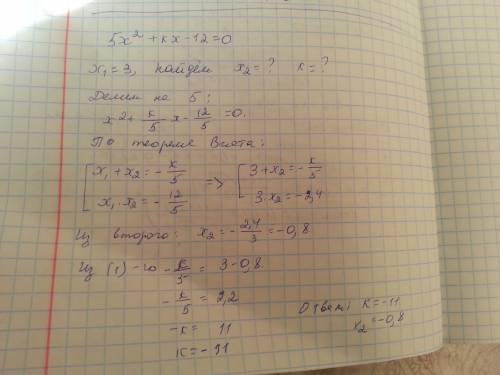
1+sinx·√(2ctgx) ≤ 0
Подкоренное выражение не может быть отрицательным
ctg x ≥ 0 0.5π ≥ x > 0 это в 1-й четверти
1.5π ≥ x > π это в 3-й четверти
в 1-й четверти sinx > 0 и выражение 1+sinx·√(2ctgx)> 0
в 3-й четверти sinx < 0 и выражение 1+sinx·√(2ctgx)может стать меньше 0, если
sinx·√(2ctgx) ≤ -1
делим на отрицательный синус
√(2ctgx) ≥ -1/sinx
обе части положительны
возводим в квадрат
2ctgx ≥ 1/sin²x
2ctgx ≥ 1 + ctg²x
1 + ctg²x - 2ctgx ≤ 0
(1 - ctgx)² ≤ 0
Квадрат любого числа не может быть отрицательным, поэтому остаётся только
равенство нулю:
1 - ctgx = 0
ctgx = 1 (четверть 3-я!)
х = 5/4π
Решение единственное: при х = 5/4π выражение 1+sinx·√(2ctgx) = 0
ну, и, разумеется следует добавить 2πn, тогда решение такое:
х = 5/4π +2πn
Школьные Знания.com
Какой у тебя вопрос?
leha2286543
5 - 9 классы Алгебра 5+3 б
От станции до озера турист доехал на велосипеде за 2 ч. Пешком он мог бы пройти это расстояние за 6 ч. Чему равно расстояние от станции до озера, если на велосипеде турист едет со скоростью, на 10 км/ч большей, чем идёт пешком?
РЕШИТЕ ЗАДАЧУ, СОСТАВИВ УРАВНЕНИЯ ДВУМЯ ОБОЗНАЧИВ БУКВОЙ КАКУЮ-НИБУДЬ СКОРОСТЬ ДВИЖЕНИЯ
2) ОБОЗНАЧИВ БУКВОЙ ИСКОМОЕ РАССТОЯНИЕ
Nhoran 17.02.2014
Отметить нарушение
ответы и объяснения
Участник Знаний
х км/ч скорость туриста пешком, (х+10) км/ч скорость туриста на велосипеде.
2(х+10)=6х; 4х=20; х=5, расстояние от станции до озера 6*5=30 км
х км расстояние от станции до озера, (х:2) км/ч скорость туриста на велосипеде, ( х:6) км/ч скорость туриста пешком, тогда (х:2)-(х:6)=10; х:3=10; х=30(км)
Нажми, чтобы рассказать другим, насколько ответ полезен
3,0
31 оценка
Не тот ответ, который тебе нужен?
НАЙДИ НУЖНЫЙ