Question

Решить: 1) составить уравнение прямой, проходящей через точку m(8; 6) и отсекает от координатного угла треугольник площадью 12 2)lim x стремится к 1( sin(1-корень из x)^2)/(x-1) 3)lim x стремится к бесконечности (корень из(3+4x^3))/(x^2+2x+3) 4)lim x стремится к 1 ((sin(x-1)^2)+(корень из(х-/(x^2-2x+1) заранее )

Answer 1

$2)\; \; \lim\limits _{x\to 1} \frac{sin^2\sqrt{1-x}}{x-1} =\Big [\frac{0}{0}\Big ]=[\; sin \alpha \sim \alpha \; ,\; \to 0\; ]=\\\\=\lim\limits _{x\to 0} \frac{(\sqrt{1-x})^2}{-(1-x)} =\lim\limits _{x\to 0} \frac{1-x}{-(1-x)} =-1\\\\3)\; \; \lim\limits _{x\to \infty } \frac{\sqrt{3+4x^3}}{x^2+2x+3} =\Big [\frac{\infty }{\infty }\Big ]= \Big [\frac{:x^2}{:x^2}\Big ]=\lim\limits _{x \to \infty} \frac{\sqrt{\frac{3}{x^4}+\frac{4}{x}}}{1+\frac{2}{x}+\frac{3}{x^2}} =\frac{0}{1}=0$

$4)\quad \lim\limits _{x \to 1} \frac{sin(x-1)^2+\sqrt{x-1}}{x^2-2x+1} =[\frac{0}{0}]=\lim\limits _{x\to 1} \frac{sin(x-1)^2}{(x-1)^2} +\lim\limits _{x\to 1} \frac{\sqrt{x-1}}{(x-1)^2} =\\\\=\lim\limits _{x\to 1} \frac{(x-1)^2}{(x-1)^2}+\lim\limits _{x\to 1} \frac{\sqrt{x-1}}{(x-1)^2} =1+\lim\limits _{x\to 1} \frac{1}{(x-1)^{3/2}} =1+\infty =\infty$

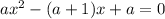
1) Используем уравнение прямой "в отрезках" :  $\frac{x}{a}+\frac{y}{b}=1$  и то, что точка М(8,6) принадлежит этой прямой. Значение площади прямоугольного треугольника  $S=\frac{ab}{2}$  .

$\left \{ {{\frac{8}{a}+\frac{6}{b}=1} \atop \frac{ab}{2}=12}} \right. \; \; ili\; \; \left \{ {{\frac{8}{a}+\frac{6}{b}=1} \atop {-\frac{ab}{2}=12}} \right. \\\\ \left \{ {{8b+6a=ab} \atop {ab=24}} \right. \; \; ili\; \; \left \{ {{8a+6b=ab} \atop {ab=-24}} \right. \\\\ \left \{ {{8b+\frac{144}{b}=24} \atop {a=\frac{24}{b}}} \right. \; \; ili\; \; \left \{ {{8b-\frac{144}{b}=-24} \atop {a=\frac{-24}{b}}} \right. \\\\1)\; \; 8b^2-24b+144=0\; |:8\\\\b^2-3b+18=0\; ,\; D\ \textless \ 0\; \; \to \; \; net\; reshenij$

$2)\; \; 8b^2+24b-144=0\; |:8\\\\b^2+3b-18=0\; ,\; b_1=-6\; ,\; \; b_2=3\\\\a_1=-\frac{24}{b}=4\; ,\; a_2=-8\\\\3)\; \; \frac{x}{4} - \frac{y}{6}=1\; \; \to \; \; 6x-4y=24\; ,\; \; \underline {3x-2y-12=0}\\\\ili\\\\ \frac{x}{-8} +\frac{y}{3} =1\; \; \to \; \; 3x-8y=-24\; ,\; \; \underline {3x-8y+24=0}$