ответ: со скорость 20 км/ч мотоциклист проедет весь путь.
Объяснение:
Пусть скорость велосипедиста х, тогда скорость мотоциклиста (х+10).
Время, за которое проезжает весь путь велосипедист 120/х, а мотоциклист 120/(х+10). Составим и решим уравнение:
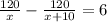
120(х+10)-120х=6х(х+10)
120х+1200-120х=6х²+60х
6х²+60-1200=0 (разделим на 6)
х²+10+200=0
D=100-4*(-200)=900, √D=30
х1=(-10+30)/2=10 км/ч скорость велосипедиста
х2=(-10-30)/2=-20-не удовлетворяет условию задачи.
10+10=20 км/ч-скорость мотоциклиста.
ответ: со скорость 20 км/ч мотоциклист проедет весь путь.
(см. объяснение)
Объяснение:
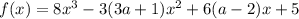
Берем первую производную:
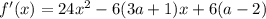
По условию нужно, чтобы имелся строгий экстремум.
Тогда берем вторую производную:
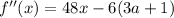
Перейдем к системе, чтобы с ее найти значения параметра, которые нужно исключить:
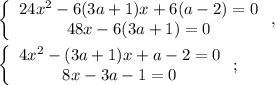
Система не имеет решений.
Вернемся к первой производной:
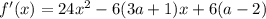
В таких случаях выгодно строить схематичную параболу, описывая каждое интересующее нас расположение на языке математики.
Учитывая, что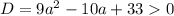 
, получим:
(см. прикрпепленный файл)
Запишем систему:
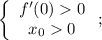
То есть нужно решить:
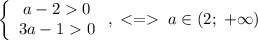
Итого при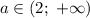 
точки экстремума функции принадлежат промежутку 
.
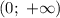Задание выполнено!
x1=-32 ; x=12