у = 5х - 3
Точка А (0; -3)
5 · 0 - 3 = -3
-3 = -3
Точка А (0; -3) принадлежит графику функции у = 5х - 3.
Точка В (-1; -4)
5 · (-1) - 3 ≠ -4
-5 - 3 ≠ -4
-8 ≠ -4
Точка В (-1; -4) не принадлежит графику функции у = 5х -3.
Точка С (0; -3)
5 · (-2) - 3 = -13
-13 = -13
Точка С (-2; -13) принадлежит графику функции у = 5х -3.
Точка М (3; 12)
5 · 3 - 3 = 12
15 - 3 = 12
12 = 12
Точка М (3; 12) принадлежит графику функции у = 5х -3.
Точка Е(0,2; -2)
5 · 0,2 - 3 = -2
1 - 3 = -2
-2 = -2
Точка Е(0,2; -2) принадлежит графику функции у = 5х -3.
Точка К (-0,4; -1)
5 · (-0,4) - 3 ≠ -1
-2 - 3 ≠ -1
-5 ≠ -1
Точка В (-0,4; -1) не принадлежит графику функции у = 5х -3.
Обобщённый ответ: графику функции у = 5х -3 принадлежат точки А(0;-3), С(-2;-13), М(3;12) и Е(0,2;-2).
Если даны три стороны, то можно найти углы треугольника по теореме косинусов.
Пусть a=6; b=25; c=29
b²=a²+c²-2·a·c·cos∠B
25²=6²+29²-2·6·29·cos∠B
cos∠B=(36+841-625)/(12·29)=21/29
BD=BC·cos∠B=6*(21/29)=126/29
По теореме Пифагора из Δ BCD высота СD
CD²=BC²-BD²=6²-(126/29)²=36-(15876/841)=14400/841
CD=120/29
( можно найти sin∠B) и
тогда
CD=BC·sin∠B
Второй
Найти площадь по формуле Герона:
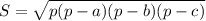
p=(a+b+c)/2 - полупериметр треугольника.
p=(6+25+29)/2=30
p-a=30-6=24
p-b=30-25=5
p-c=30-29=1
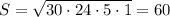
Наименьшая высота проведена к наибольшей стороне.
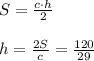
Пусть х(км/ч)-собственная скорость лодки (т.е. скорость в стоячей воде), тогда скорость лодки по течению (х+2)км/ч, а против течения (х-2)км/ч. Время движения лодки по течению 28/(х+2)ч, против течения 25/(х-2)ч, в стоячей воде 54/х (ч). По условию лодка затратила на весь путь по течению и против течения столько же времени сколько на путь в стоячей воде. Составим и решим уравнение:
28/(х+2)+25/(х-2)=54/х, ОДЗ: х- не равен -2, 2, 0.
28х(х-2)+25х(х+2)=54(х-2)(х+2),
28х^2-56х+25х^2+50х=54х^2-216,
28х^2+25х^2-54х^2-6х+216=0,
-х^2-6х+216=0,
х^2+6х-216=0,
Д=9+216=225, 2 корня
х=-3+15=12
х=-3-15=-18-не явл. решением
12(км/ч)-скорость лодки в стоячей воде
ответ:12км/ч