Графики обратных функции симметричны относительной прямой y=x.
Чтобы построить обратную функцию к f(x), надо для каждой точки графика функции y=f(x) найти симметричную, относительно прямой y=x. (см. приложение) Для этого надо провести перпендикуляр от точки к y=x, длина которого в два раза больше, чем расстояние от точки до прямой y=x, и на другом конце перпендикуляра отметить новую, симметричную точку.
Безусловно для каждой точки сделать сложно (если графиком f(x) не является какая-то прямая/ломанная), поэтому обычно это делают для точек в которых: 1. График пересекает оси координат; 2. Функция меняет монотоность. И если между точками Δy в несколько раз отличается от Δx (функция быстро убывает/возрастает).
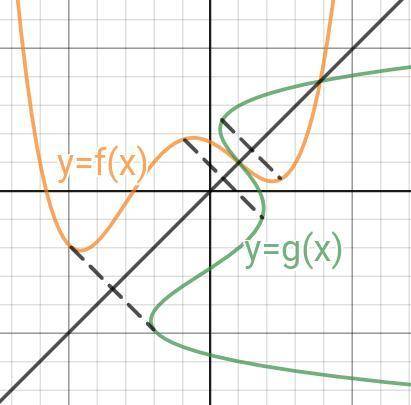
решение достаточное легкое, прикрепляю фото, но еще и объясню на словах, чтобы было понятнее. На фото более краткий разбор, нужно только оформить, а этот текст просто чтобы понять что к чему и не запутаться)
Нам дан равнобедренный треугольник АВС, мы проводим высоту ВК, которая равна 67. Она отделяет два прямоугольных треугольника АВК и ВКС, тк нам нужно найти АВ, то мы будем рассматривать треугольник АВК. Угол АВК будет равен половине угла АВС, тк высота ВК делит угол В пополам. 120:2= 60. Угол ВКА равен 90 градусов, тк Вк высота. Сумма всех углов треугольника равна 180. складываем известные нам углы в треугольнике АВК, сумма которых равно 150. 180-150=30, делаем вывод что угол ВАК = 30 градусов. По свойству прямоугольного треугольника (Катет, лежащий против угла 30градусов, равен половине гипотенузы.) делаем вывод, что ВК равен половине АВ (ВК - катет, лежит напротив угла 30 гр, АВ - гипотенуза). Следовательно, гипотенуза АВ=2ВК. 67*2=134.
АВ=134.

D = 25 + 4•2•3 = 25 + 24 = 49 = 7²
x1 = (-5 + 7)/6 = 2/6 = 1/3.
x2 = (-5 - 7)/6 = -12/6 = -2.
б) x² - 2x - 1 = 0
x² - 2x + 1 - 2 = 0
(x - 1)² - 2 = 0
(x - 1 - √2)(x - 1 + √2) = 0
x = 1 + √2
x = 1 - √2.
в) 4x² - 12x + 9 = 0
(2x)² - 2•2•3x + 3² = 0
(2x - 3)² = 0
2x = 3
x = 1,5.