ответ:6
Объяснение:1. Заметим, что никакое число, не превосходящее 1015, не может иметь высоту 4. Действительно, наименьшее число высоты 4 — это
2222=216, при этом это число больше 1015.
2. Между тем числа высоты 3, не превосходящие 1015, существуют. Например, 16=222 имеет высоту 3. Таким образом, задача свелась к подсчёту количества чисел высоты 3, не превосходящих 1015.
3. Заметим, что
29≤1015≤210,
36≤1015≤37,
44≤1015≤45,
54≤1015≤55,
63≤1015≤64.
4. Найдём количество чисел высоты 3, не превосходящих 1015. Это то же самое, что найти количество решений неравенства:
x1x2x3≤1015, xi≥2.
Если x1=2, то x2x3≤9, отсюда x2=x3=2, или x2=2, x3=3, или x2=3, x3=2. Отсюда получаем 3 решения.
Далее, если x1=3,4,5, получаем, что x2=x3=2, что даёт ещё три решения.
Наконец, при x1≥6 получаем, что x2x3≤3. Но так как xi≥2, то таких x2, x3 не существует.
5. Таким образом, получаем 3+3=6 чисел максимальной высоты, не превосходящих 1015.
, 
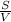= 4 часа — время, потраченное легковой машиной на путь. 
Привет!
вот первый график
смотри на неком участке функция меняет знак и значение это промежуток 4 ≥ x ≥ -5
т. к если мы раскроем модули
при x ≤ -5
y = - ( x + 5 ) + ( x - 4) = -9 т.е значение функции постоянно тк не зависит от х
при x ≥ 4
y= (x+5 ) - ( x-4) = 9 аналогично ↑
рассмотрим 4 ≥ x ≥ -5
y = (x+5) + ( x - 4 ) = 2x -1 график функции на этом промежутке прямая 2x -1