(-бесконечности ; -10] и (7; +бесконечности)
Объяснение:
Запишем все под одной дробью:
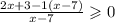
Найдём область допустимых значений:
х-7≠0, то есть х ≠ 7
Раскроем скобки и решим:
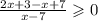
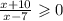
Рассмотрим все возможные случаи (знаменатель строго больше нуля, так как если он будет равен нулю, выражение потеряет смысл):
1. Когда и знаменатель, и числитель больше 0
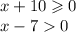
2. Когда оба меньше 0
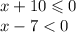
1.
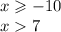
То есть х принадлежит ( 7; +бесконечности)
Так как 7 не удовлетворяет ОДЗ, то скобки круглые
2.
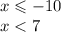
То есть х принадлежит (- бесконечности ; - 10]
Найдём объединение:
Х принадлежит (-бесконечности ; -10] и (7; +бесконечности)
Всего три пары - 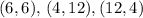
Объяснение:
Для того чтобы решить задачу, нужно правильно сформулировать проблему -
"Требуется найти все пары 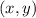 , где
, где 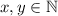 так что
так что 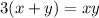 ."
."
Из равенства 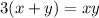 очевидно что
очевидно что 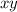 делится на 3. Следовательно хотя бы одно из чисел
делится на 3. Следовательно хотя бы одно из чисел 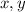 делится на 3. Без огранчения общности, предположим что
делится на 3. Без огранчения общности, предположим что 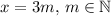 .
.
Следовательно, высшеупомянотое равенство преообразовывается в
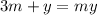 , из которого выводим
, из которого выводим 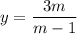 .
.
Заметим что отсюда выходит что, 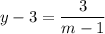 .
.
Т.к. 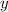 цело только и только тогда, когда
цело только и только тогда, когда 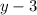 цело, то следовательно, 3 должно делится на
цело, то следовательно, 3 должно делится на  .
.
Число 3 делится только на четыре числа - 3, -3, 1, -1. Но лишь только два из них подходят - 3 и 1.
Следовательно,
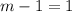 или
или 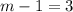 .
.
Т.е.,
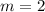 или
или 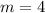
Отсюда получаем две пары - 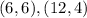 . Однако очевидно, что также и пара
. Однако очевидно, что также и пара 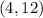 подходит.
подходит.