Пусть второй рабочий изготовил х деталей. Первый рабочий изготовил на 16% больше. Чтобы найти 16% от числа х, надо 16% перевести в десятичную дробь 0,16, а чтобы найти дробь от числах, надо это число х умножить на дробь 0,16. Значит, первый рабочий изготовил (х + 0,16х) деталей. Вместе оба рабочих изготовили (х + (х + 0,16х)) деталей или 86 деталей. Составим уравнение и решим его.
x + (x + 0,16x) = 86;
x + x + 0,16x = 86;
2,16x = 86;
x = 86 : 2,16;
x = 39,8=40 (деталей) – второй рабочий;
x + 0,16x = 1,16x = 40 * 1,16 = 46 (деталей) – первый рабочий.
ответ. 40 деталей; 46 деталей.
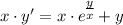
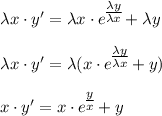
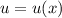с замены:
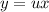, тогда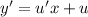 
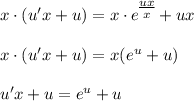
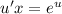
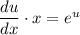- уравнение с разделяющимися переменными.
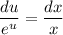- уравнение с разделёнными переменными.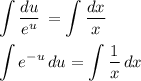
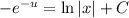- общий интеграл новой функции.
из решения уравнения с разделяющимися переменными, чтобы записать решение исходного однородного уравнения, остаётся выполнить обратную замену: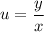 
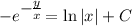- общий интеграл исходного уравнения.
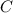. Подставим в общий интеграл начальное условие: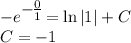
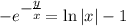- частный интеграл, также является решением данного дифференциального уравнения.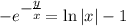
(5√7 -13)(5√7 +13)=(5√7)²-13²=5² *(√7)²-169=25*7-169=175-169=6
ответ: 6