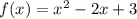
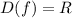

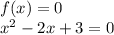


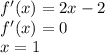
a) функция - композиция дробно-рациональной
t(x)=1/(x-1) и показательной y=7^(t(x))
t(x)=1/(x-1) - непрерывна при х∈(-∞;1) U(1;+∞)
y=7^(t(x)) - непрерывна при t∈(-∞;+∞)
Значит и данная функция непрерывна при x∈(-∞;1) U(1;+∞)
Проверяем непрерывность в точке x=1
Находим предел слева: lim (x→1-0)7^(1/(x-1))=0
x→1-0 тогда (1/(x-1))→-∞
7^(-∞)→0
Находим предел справа:lim (x→1+0)7^(1/(x-1))=+∞
x→1+0 тогда (1/(x-1))→+∞
7^(+∞)→+∞
x=1- точка разрыва второго рода ( один из односторонних пределов - бесконечный)
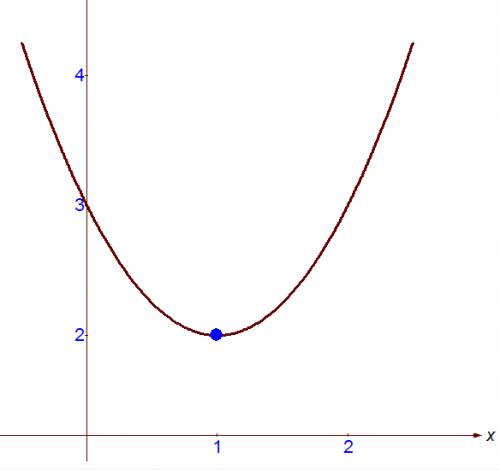
б) y=x² непрерывна на (-∞;+∞), а потому непрерывна и на [0;1]
y=2x+3 непрерывна на (-∞;+∞), а потому непрерывна и на (1;2]
Значит, надо исследовать непрерывность в точке х=1
Находим предел слева: lim (x→1-0)x²=(1-0)²=1
Находим предел справа:lim (x→1+0)7=2·1+3=5
Предел слева не равен пределу справа.
Значит предел функции в точке не существует и потому
x=1- точка разрыва первого рода ( пределы конечны, но не равны, есть конечный скачок)
√(x²+2*3*x+3²)=2
√(x+3)²=2
|x+3|=2
Раскрываем модуль, получаем систему уравнений:
x+3=2 x₁=-1
-x-3=2 x₂=-5
ответ: x₁=-1 x₂=-5.