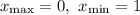Объяснение:
A1.
a) (5a+10)/(b-7):(a²+4a+4)/2b-14=(5(a+2)/(b-7) * ((2(b-7))/(a²+4a+4)=
=(5(a+2)2(b-7))/((b-7)(a+2)²)=5*2/(a+2)=10/(a+2)
a²+4a+4=0; D=16-4*1*4=0
a₁=a₂=0,5(-4±√0)= -2
a²+4a+4=(a+2)(a+2)=(a+2)²;
б) (√50-√6)/√12=(√(25*2)-√(3*2))/(√3*2*2)=(5√2-√(3*2))/(√3*2*2)=
=(5-√3)/√6=(√6(5-√3)/6=(5√(3*2)-√(3*3*2))/6=(5√6-3√2)/6.
A2.
а) (√2)⁶/32=(2¹⁽²)⁶/2⁵=2³/2⁵=2³⁻⁵=2⁻²=1/2²=1/4;
б) (5,2*10⁻⁷)(3,5*10⁴)=5,2*3,5*10⁻⁷⁺⁴=18,2*10⁻³=1/(18,2*10³);
в) 3⁻⁶*9⁻²/(3⁻¹²)=3⁻⁶*(3²)⁻²/3⁻¹²=3⁻⁶*3⁻⁴/3⁻¹²=3⁻¹⁰/3⁻¹²=3⁻¹⁰⁻⁽⁻¹²⁾=3⁻¹⁰⁺¹²=3²=
=9.
А3.
x²+2x=16x-49;
x²+2x-16x+49=0;
x²-14x+49=0;
x²-2*7x+7²=0;
(x-7)²=0;
x₁=x₂=7.
B1.
x³-3x²-4x+12=0;
(x³-3x²)-(4x-12)=0;
x²(x-3)-4(x-3)=0;
(x-3)(x²-4)=0;
x-3=0; x=3;
x²-4=0; x²=4; x=±√4; x=±2;
x₁=-2; x₂=2; x₃=3
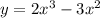
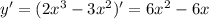
Необходимые условия экстремума:
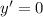
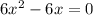
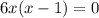
Имеем две критические (стационарные) точки: 
и 
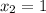
Достаточные условия экстремума: если при переходе через критическую точку производная непрерывной функции меняет знак на противоположный, то имеем экстремум функции в этой точке.
Если точка с абсциссой 
меняет знак с "+" на "–" (двигаясь в направлении увеличения 
), то — точка максимума, а если с "–" на "+" , то — точка минимума.
Из промежутка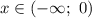 
выберем, например, 
и имеем: 
Из промежутка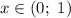 
выберем, например, 
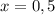и имеем: 
Имеем максимум в точке с абсциссой 
Из промежутка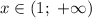 
выберем, например, 
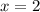и имеем: 
Имеем минимум в точке с абсциссой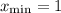 
ответ: 
