Начертите треугольники ! #171 на продолжении медианы md треугольника klm отложен отрезок da=md, а на продолжении медианы kf отложен отрезок fe=kf. докажите, что точка a,l,e лежат на одной прямой. #174 в 170 прямая b, проходящая через точку о, пересекает прямые m и n в точках e и f; ec=12см. найдите отрезок df.

👇

Ответ:

filip198585

15.08.2020

#171.
Соединим точки М и Е отрезком МЕ, а точки К и А отрезком КА.
Рассмотрим четырехугольник КLEM. В нём точкой пересечения F
диагонали KE и LM делятся пополам: КF=FE (по условию задачи)
и LF=FM (КF - медиана треугольника KLM).
Следовательно, этот четырёхугольник - параллелограмм и КМ║LE.
Рассмотрим четырёхугольник KALM. В нём точкой пересечения D диагонали AM и KL делятся пополам: DA=MD (по условию задачи) и
KD=DL (MD - медиана треугольника KLM).
Следовательно, этот четырёхугольник - параллелограмм и KM║AL.
Так как LM и AL║KM, отрезок А(L)Е║КМ, а точки A, L, E ∈ прямой АЕ.
#174.
Проведём через точку О (середина отрезка CD) прямые FN и EM (Точки F и M лежат на прямой m, а точки E и N лежат на прямой n).
Рассмотрим ΔСОМ и ΔЕОD. ∠COM=∠EOD (как вертикальные) ∠OED=∠CMO
(как накрест лежащие) и CO=OD (по условию задачи) ⇒ ΔCOM=ΔEOD.
Поэтому OV=OE. Аналогично рассмотрев ΔCOF и ΔNOD доказываем их равенство. Поэтому OF =ON.

4,5(80 оценок)

Открыть все ответы

Ответ:

elenafilatova11

15.08.2020

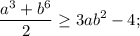
$$ \frac{a^3+b^6}{2}\geq 3ab^2-4;$

Вспоминаем неравенство Коши

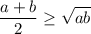
$$\frac{a+b}{2}\geq \sqrt{ab}$

Применяем:

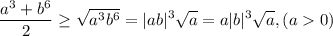
$$\frac{a^3+b^6}{2}\geq \sqrt{a^3b^6}=|ab|^3\sqrt{a}=a|b|^3\sqrt{a}, (a0)$

Покажем, что правое выражение здесь не меньше правого выражения в исходном неравенстве, тогда правое выражение в исходном неравенстве тем более будет не меньше, чем левое в исходном.

Это как если надо доказать, что a>b, мы доказали, что при a>c выполняется c>b, то точно a>b (транзитивность неравенств).

Делаем это:

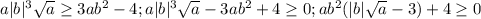
$a|b|^3\sqrt{a}\geq 3ab^2-4; a|b|^3\sqrt{a}-3ab^2+4\geq 0; ab^2(|b|\sqrt{a}-3)+4\geq 0$

Это неравенство аналогично неравенству 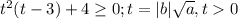$t^2(t-3)+4\geq 0; t=|b|\sqrt{a}, t0$

Чтобы решить это неравенство, надо найти нули функции

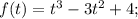f(t)=t^3-3t^2+4; , здесь сумма коэффициентов при нечетных степенях (1) равна сумме коэффициентов при нечетных степенях (-3+4=1), значит, t=-1 - корень. Поделив уголком на t+1 или по схеме Горнера, получим разложение t^3-3t^2+4=(t+1)(t^2-4t+4)=(t+1)(t-2)^2

Теперь можно решать неравенство, при этом по методу интервалов, так как при t везде коэффициент равен 1, в самом правом промежутке будет "+", а в остальных случаях при переходе через нули будет чередоваться, кроме нулей четности, как здесь t=2 (2-я степень при скобке), знаки будут - + +

Тогда $(t+1)(t-2)^2\geq 0 \Rightarrow t \in[-1;2]\cup[2;+\infty) \Rightarrow t \in [-1;+\infty)$

Но мы рассматриваем только t>0, а там везде неравенство выполняется, значит, выполняется и неравенство 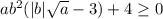$ab^2(|b|\sqrt{a}-3)+4\geq 0$ , то есть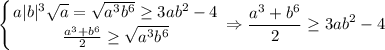 $$\left \{ {{a|b|^3\sqrt{a}=\sqrt{a^3b^6}\geq 3ab^2-4} \atop {\frac{a^3+b^6}{2}\geq \sqrt{a^3b^6} }} \right. \Rightarrow \frac{a^3+b^6}{2} \geq 3ab^2-4$

Что и требовалось доказать (естественно, неравенство справедливо по условию с ограничением a>0)

4,7(61 оценок)

Ответ:

Papitto

15.08.2020

Число будет четным, если последняя цифра четная. В данном случае четырёхзначное число будет четным, если последняя цифра будет 6 или 8.

№1) Пусть последняя цифра будет 6, тогда на первое место можно использовать 3 цифры, на второе место - оставшиеся из 2 цифр и на треть место - 1 цифра.

По правилу произведения, таких четырёхзначных чисел: 3*2*1*1=6

Пусть теперь последней цифро будет 8. Аналогично с №1) получим, что четных таких чисел будет 6.

И по правилу сложения всего таких четырёхзначных чисел можно составить

4,6(86 оценок)

Это интересно:

Компьютеры-и-электроника

03.09.2021

11 способов, как экономить ресурсы в игре Clash of Clans...

Кулинария-и-гостеприимство

15.05.2021

Как заготовить розмарин: собираем и храним ароматные травы впрок...

Праздники-и-традиции

28.09.2020

8 советов о том, как купить подарки на Рождество, если у вас немного денег...

Компьютеры-и-электроника