Даны два числа 1)2 и 3; 2)2 и 1/3.составьте несколько квадратных трехчленов,имеющих своими корнями эти - id706308620201017 от darytish 17.10.2020 12:23

Question

Алгебра: Даны два числа 1)2 и 3; 2)2 и 1/3.составьте несколько квадратных трехчленов,имеющих своими корнями эти числа.

darytish · Accepted Answer

Экстремумы на отрезке находятся либо в стационарных точках (точках, где производная функции обращается в ноль), либо на концах отрезка.

Для этого сначала нужно найти производную функции. Если я правильно поняла запись Вашей функции и она такая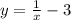 $y=\frac{1}{x}-3$

То ее производная равна -1/х^2

Критической точкой здесь будет х=0. Но наша функция в этой точке не существует. Значит экстремумы находятся на концах отрезка:

у(-1)=-4

у(1)=-2

Значит минимальное значение функция достигает в точке х=-1 и равна -4.

Максимальное значение функции на отрезке равно -2 и находится в точке х=1.

Даны два числа 1)2 и 3; 2)2 и 1/3.составьте несколько квадратных трехчленов,имеющих своими корнями эти числа.