1. Подставим координаты начала координат, то есть точки (0; 0) в уравнение:
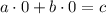
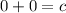

Значит, при c=0 прямая с уравнением ax+by=c проходит через начало координат.
Для ответа на следующие вопросы представим уравнение прямой в виде уравнения с угловым коэффициентом:
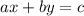
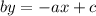
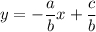
2. Заданное уравнение прямой также представим в виде уравнения с угловым коэффициентом:
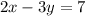
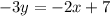
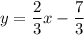
Две прямые параллельны, когда равны их угловые коэффициенты. То есть должно выполняться условие:
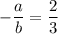
Переписать это можно, например, так:
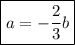
3. Снова заданное уравнение прямой представим в виде уравнения с угловым коэффициентом:
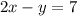
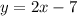
Две прямые перпендикулярны, когда их угловые коэффициенты обратны по модулю и противоположны по знаку. То есть должно выполняться условие:
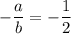
Переписать это можно в виде:
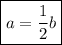
sin²π - cos²(-π) +sin ²(-2π)= cos²2π
-cos²(-π) = +cos²π
sin²π+cos²π=1
1+sin ²(-2π)=1-sin ²(2π) = cos²2π