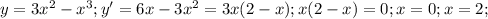- две критические точки в области определения R. 
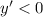на промежутках 
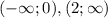и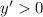 
на промежутке 
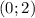, значит функция 
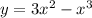убывает на промежутках 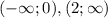и возрастает на промежутке . 
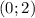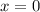- точка минимума, 
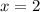- точка максимума. 
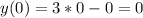- значение минимума функции, 
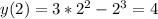- значение максимума функции.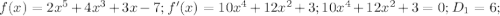
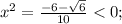- корней нет, 
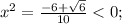- корней нет.
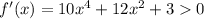при любых х, то функция 
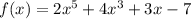возрастает в области определения R.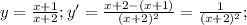
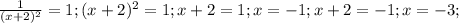
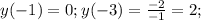
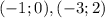- точки, в которых касательная параллельна прямой у=х-3.
Определение. Высказыванием называется утверждение, которое является истинным или ложным (но не одновременно).
То есть, чтобы выяснить, является ли некоторое предложение высказыванием, нужно сначала убедиться, что это утверждение, а затем установить, истинно оно или ложно.
Пример. “Москва – столица России” – истинное высказывание.
“5 –четное число” – ложное высказывание.
“” – не высказывание (неизвестно, какие значения принимает ).
“Студент второго курса” не высказывание (не является утверждением).
Высказывания бывают элементарные и составные.
Элементарные высказывания не могут быть выражены через другие высказывания. Составные высказывания можно выразить с элементарных высказываний.
Пример. “Число 22 четное” – элементарное высказывание.
“Число 22 четное и делится на 11” – составное высказывание.
Высказывания обозначают заглавными буквами латинского алфавита: , , ,… Эти буквы называют логическими Атомами.
При фиксированном множестве букв Интерпретацией называется функция , которая отображает множество во множество истинностных (логических) значений , то есть .
Истинностные значения истина и ложь сокращенно обозначаются и, л или T, F, или 1,0. Мы будем использовать обозначения 1 и 0. В определенной интерпретации буквы принимают значения 1 или 0.
К высказываниям и буквам можно применять известные из курса дискретной математики логические связки или логические операции. При этом получаются Формулы (формы). Формулы становятся высказываниями при подстановке всех значений букв.