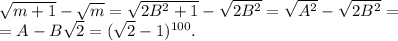![S=6\cdot \frac{1}{2}\cdot R^2\cdot sin60^\circ=3\cdot R^2\cdot \frac{\sqrt3}{2}=\frac{3\sqrt3\cdot R^2}{2}=72\sqrt2\; \; \; \Rightarrow \\\\R^2=\frac{2\cdot 72\sqrt2}{3\sqrt3}=\frac{48\cdot \sqrt2}{\sqrt3}=\frac{48\cdot \sqrt2\cdot \sqrt3}{3}=16\sqrt6\\\\R=\sqrt{16\sqrt6}=4\sqrt[4]{6}\\\\\\l_{okryznosti}=2\pi R=2\pi \cdot 4\sqrt[4]6=8\pi \sqrt[4]6](/tpl/images/0714/2192/23cd4.png)
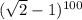раскрыть 100-ую степень по биному Ньютона, то получится сумма слагаемых вида 
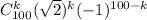по k от 0 до 100. При четных k эти слагаемые будут натуральными числами, а при нечетных k они имеют вид 
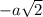, где а - натуральное. Значит, 
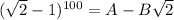, при некоторых натуральных 
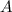и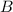 
. (для решения задачи нет нужды их явно вычислять). Опять же из бинома Ньютона понятно, что тогда 
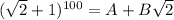, т.к. в нем будут те же слагаемые, только все со знаком плюс. Перемножив эти два соотношения, получим 
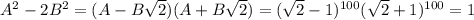, то есть 
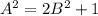. Поэтому, если положим 
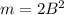, то получим, что 
