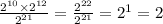
Если непонятно, как так получилось:
У нас в числителе умножаются числа 2 в 10 степени и 2 в 12 степени. При умножении двух чисел с одинаковыми основаниями степени складываются, то есть у нас будет 2 в степени 10+12, получается 2 в 22 степени
Смотрим сейчас:
В числителе у нас 2 в 22 степени, в знаменателе 2 в 21. А дробная черта - это что? Это деление. То есть, по сути, у нас 2 в 22 степени делится на 2 в 21 степени. При делении чисел с одинаковыми основаниями степени вычитаются. То есть, в итоге у нас получится 2 в степени 22-21, получаем 2 в 1 степени, то есть просто 2
Область определения функции. ОДЗ: -00<x<+00
Точка пересечения графика функции с осью координат Y:График пересекает ось Y, когда x равняется 0: подставляем x=0 в x^2+4*x+3.
Т.к. cos(x) не ноль, то разделим уравнение на cos^2(x):
sin^2(x)/cos^2(x) + sin(x)/cos(x) - 2 = 0, т.е. tg^2(x) +tg(x) - 2 = 0
Сделаем замену t = tg(x)
t^2 + t - 2 = 0
D = 1 + 8 = 9
t1 = (-1-3)/2 = -2
t2 = (-1+3)/2 = 1
Обратная замена:
tg(x) = 1, отсюда x = p/4 + n*p
tg(x) = -2, x = arctg(-2) + n*p