х= 2 и у =2
х+2у+ху=10
+
х+2у-ху=2
после добавление выходит
2х+4у=12 /2
х+2у=6
и еще
х+у =10-ху и х+у =2+ ху
преравняем
10-ху=2+ху
ху=4
подбираем : х=2 и у =2!
как то так:)
В решении.
Объяснение:
1) Решить неравенство:
3х² <= 12
Решить как квадратное уравнение:
3х² = 12
х² = 4
х = ±√4
х = ± 2.
х = -2 и х = 2 - точки пересечения параболой оси Ох.
Построить график у = 3х² - 12
Определить по графику, при каких значениях х у <= 0.
По графику ясно видно, что у <= 0 при х от -2 до 2.
Решение неравенства: х∈[-2; 2], пересечение.
Неравенство нестрогое, скобки квадратные.
2) Решить неравенство:
х²/3 > 3
Решить как квадратное уравнение:
х²/3 = 3
х² = 9
х = ±√9
х = ± 3.
Построить график у = х² - 9.
Определить по графику, при каких значениях х у > 0.
По графику ясно видно, что у > 0 при х от -∞ до -3 и от 3 до + ∞.
Решение неравенства: х∈(-∞; -3)∪(3; +∞), объединение.
Объяснение:
1) построим графики y=3x² и у=12
из точки пересечения графиков проведем отрезки перпендикулярно оси ОХ
точки пересечения перпендикуляра к оси ОХ определяют отрезок на оси ОХ являющийся решением
х∈[-2;2]
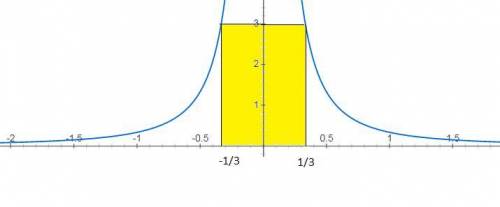
2) построим график y=1/(3x)²
и у=3
из точки пересечения графиков проведем отрезки перпендикулярно оси ОХ
точки пересечения перпендикуляра к оси ОХ определяют отрезок на оси ОХ являющийся решением
х∈(-1/3;1/3)

сложим уравнения получим x+2y=6 или x=6-2y
вычтем уравнения получим xy=4 подставим x,
получим y^2-3y+2=0
решаем y=2 y=1
x=6-2*2=2
x=6-2*1=4
(2;2) (4;1)