2/3; 2
Объяснение:
3y^2-8y+4=0
D=(-8)^2-4*3*4=64-48=16
В уравнении 2 корня, значит
x1 = (-(-8) +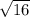 
)/(2*3) = 12/6 = 2 - первый корень
x2 = (-(-8) - 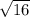)/(2*3) = 4/6 = 2/3 - второй корень
Как найти дискриминант?
1) Дискриминант квадратного уравнения ax^2+bx+c находится по формуле: b^2-4ac. a; b и c - коэффициенты. В данном случае a=3; b=-8; c=4.
2) Подставляем: D=(-8)^2-4*(3*4)=64-48=16
3) Если D>0, то в уравнении 2 корня, если D=0, то в уравнении 1 корень, если D<0, то в уравнении корней нет
Как найти корни?
Опять же таки берём уравнение вида ax^2+bx+c
Если D>0, то x1 = (-b+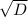
)/2a
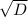x2 = (-b-)/2a
Если D=0, то x = -b/2a
Если D<0, то ничего не ищем
P.S. Также есть теоремы Виета и выделения полного квадрата, но они более замороченные. Конечно, проще решать через дискриминант, но если вы хотите увидеть, как решить уравнение другим напишите, я отредактирую ответ, попробую решить другим
ответ: 360
Объяснение:
Перепишем число следующим образом:
A = 10^50(10^10 -1) + 10^30(10^10 -1) + 10^20 - 1
Число 10^10 - 1 состоит из 10 цифр 9 подряд, а число 10^50(10^10 -1) тоже самое, только + еще 50 ноликов в хвосте. Соответственно 10^30(10^10 -1) тоже самое, только уже 30 ноликов в хвосте.
Число: 10^50(10^10 -1) имеет в хвосте ровно 50 нулей, а число 10^30(10^10 -1) имеет 40 цифр, при этом 40<50, то есть при сложении этих чисел, последнее просто вписывается в хвост взамен 40 последних нулей первого числа. Аналогично, при сложении к этим двум числам, числа 10^20 - 1, состоящего из 20 девяток, то есть оно приписывается в конец, заменяя 20 последних нулей ( 20<30).
Как видим, сумма цифр такого числа : 9*(10 + 10 + 20) = 9*40 = 360
20*2.5 = 50 рублей стоимость авторучки