Question

2показательных уравнения - 80

Answer 1

9^(x-0,5) - 10*3^(x-2) + 1/3 ≤ 0

9^x/3 - 10*3^x/9 + 1/3 ≤ 0

для красоты умножим левую и правую часть на 9 и 9^x = 3^(2x)

3*3^(2x)  - 10*3^x + 3 ≤ 0

3^x = t > 0

3t^2 - 10t + 3 ≤ 0

D = 100 - 4*3*3 = 64 = 8²

t12=(10+-8)/6 = 1/3   3

(3t - 1)(t - 3) ≤ 0

применяем метод интервалов

[1/3] [3]

t ≥ 1/3  

t ≤ 3

1. t ≥ 1/3

3^x ≥ 3^(-1)

x ≥ -1

2. t ≤ 3

3^x ≤ 3

x ≤ 1

ответ x∈ [-1, 1]

3*9^x - 8*15^x + 25^(x+0.5) ≥ 0

делим левую и правую части на 25^x (положительное число)

3*(9/25)^x - 8*(15/25)^x + 5 ≥ 0

3*(3/5)^(2x) - 8*(3/5)^x + 5 ≥ 0

(3/5)^x = t >0

3t^2 - 8t + 5 ≥ 0

D = 64 - 60 = 4 = 2²

t12 = (8+-2)/6 = 5/3   1

(t - 1)(3t - 5) ≥ 0

применяем метод интервалов

[1] [5/3]

t ≤ 1

t ≥ 5/3

1. t ≤ 1

(3/5)^x ≤ 1 = (3/5)^0

основание меньше 1 - знак неравенства меняется

x ≥ 0

2. t ≥ 5/3

(3/5)^x ≥ (3/5)^(-1)

основание меньше 1, знак меняется

x ≤ -1

ответ x∈(-∞, -1] U [0, +∞)

Answer 2

1. $\frac{(3^x)^2}{9^{\frac{1}{2} }} -10*\frac{3^x}{3^2}+\frac{1}{3}\leq 0; \frac{1}{3}(3^x)^2-\frac{10}{9}*3^x+\frac{1}{3}\leq 0; t=3^x; t0;\\ \frac{1}{3}t^2-\frac{10}{9}t+\frac{1}{3}\leq 0; 3t^2-10t+3\leq 0;$

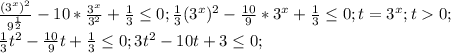
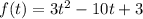
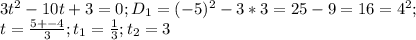
Теперь решим квадратное неравенство относительно t. Ограничение пока не трогаем. Решаем методом интервалов, для этого найдем нули функции $f(t)=3t^2-10t+3$

$3t^2-10t+3=0; D_1=(-5)^2-3*3=25-9=16=4^2;\\ t=\frac{5+-4}{3};t_1=\frac{1}{3}; t_2=3$

Переходим к неравенству. 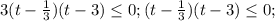$3(t-\frac{1}{3})(t-3)\leq 0; (t-\frac{1}{3})(t-3)\leq 0;$

В таком разложении есть важная особенность: знаки нам здесь можно и не проверять, так как во всех скобках при t коэффициент 1 и поэтому в правом промежутке будет "+", а дальше они будут чередоваться, так как при скобках нет четных степеней (т.е. у f(t) нет нулей четной кратности).

Имеем $\boxed {t \in [\frac{1}{3};3]}$ или $\frac{1}{3} \leq t \leq 3; \left \{ {{t \geq \frac{1}{3} } \atop {t \leq 3}} \right.$

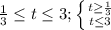
Делаем обратную замену:$\left \{ {{3^x \geq 3^{-1}} \atop {3^x \leq 3^1}} \right. \Rightarrow \left \{ {{x \geq -1} \atop {x \leq 1}} \right. \Rightarrow x \in[-1;1]$

Знаки не менялись, потому что 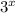$3^x$ -  монотонно возрастающая функция (3>1).

ответ: $\boxed {x \in[-1;1]}$

2. $3*(3^x)^2-8*3^x*5^x+5*(5^x)^2\geq 0$

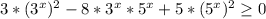
Напоминает тригонометрию, где слева квадрат синуса, например, а справа - квадрат косинуса. Решается делением на квадрат правого. В данном случае это 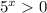$5^x0$, поэтому знак неравенства не поменяется.

$3*((\frac{3}{5})^x )^2-8*(\frac{3}{5} )^x+5\geq 0; t=(\frac{3}{5})^x; t0;\\ 3t^2-8t+5\geq 0$

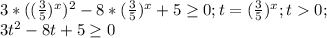
Решать будем снова методом интервалов, снова пока на ограничение не смотрим. Найдем нули 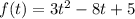$f(t)=3t^2-8t+5$

Сразу видно, что сумма коэффициентов в уравнении 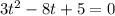$3t^2-8t+5=0$ равна 0 (3-8+5=0), следовательно, 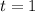$t=1$ - один корень, а второй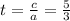 $t=\frac{c}{a}=\frac{5}{3}$

Теперь имеем:

$3(t-1)(t-\frac{5}{3})\geq 0; (t-1)(t-\frac{5}{3})\geq 0$

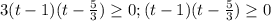
Здесь снова при t коэффициенты равны 1, в правом промежутке (с +∞) знак "+", а дальше чередование.

$\boxed {t \in (-\infty;1]\cup[\frac{5}{3}; +\infty)}$

По-другому мы можем это записать таким образом:

$\left [ {{t\frac{5}{3} }} \right.$

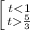
Делаем обратную замену:

$\left [ {{(\frac{3}{5})^x\leq (\frac{3}{5})^0 } \atop {(\frac{3}{5})^x\geq (\frac{3}{5})^{-1} }} \right. ;$

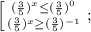
Вот здесь надо понимать, что 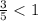$\frac{3}{5}$, функция 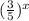$(\frac{3}{5})^x$ - монотонно убывающая, поэтому знаки придется менять.

Тогда получим:

$\left [ {{x \geq 0} \atop {x \leq -1}} \right. \Rightarrow x \in (-\infty;-1] \cup [0;+\infty)$

ответ: $\boxed {x \in (-\infty;-1] \cup [0;+\infty)}$