Question

Доказать, что при a> 0

(a³+ b^6) / 2 ≥ 3ab² - 4

Answer 1

$$ \frac{a^3+b^6}{2}\geq 3ab^2-4;$

Вспоминаем неравенство Коши

$$\frac{a+b}{2}\geq \sqrt{ab}$

Применяем:

$$\frac{a^3+b^6}{2}\geq \sqrt{a^3b^6}=|ab|^3\sqrt{a}=a|b|^3\sqrt{a}, (a0)$

Покажем, что правое выражение здесь не меньше правого выражения в исходном неравенстве, тогда правое выражение в исходном неравенстве тем более будет не меньше, чем левое в исходном.

Это как если надо доказать, что a>b, мы доказали, что при a>c выполняется c>b, то точно a>b (транзитивность неравенств).

Делаем это:

$a|b|^3\sqrt{a}\geq 3ab^2-4; a|b|^3\sqrt{a}-3ab^2+4\geq 0; ab^2(|b|\sqrt{a}-3)+4\geq 0$

Это неравенство аналогично неравенству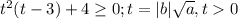 $t^2(t-3)+4\geq 0; t=|b|\sqrt{a}, t0$

Чтобы решить это неравенство, надо найти нули функции

$f(t)=t^3-3t^2+4;$, здесь сумма коэффициентов при нечетных степенях (1) равна сумме коэффициентов при нечетных степенях (-3+4=1), значит, t=-1 - корень. Поделив уголком на t+1 или по схеме Горнера, получим разложение $t^3-3t^2+4=(t+1)(t^2-4t+4)=(t+1)(t-2)^2$

Теперь можно решать неравенство, при этом по методу интервалов, так как при t везде коэффициент равен 1, в самом правом промежутке будет "+", а в остальных случаях при переходе через нули будет чередоваться, кроме нулей четности, как здесь t=2 (2-я степень при скобке), знаки будут - + +

Тогда $(t+1)(t-2)^2\geq 0 \Rightarrow t \in[-1;2]\cup[2;+\infty) \Rightarrow t \in [-1;+\infty)$

Но мы рассматриваем только t>0, а там везде неравенство выполняется, значит, выполняется и неравенство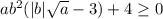 $ab^2(|b|\sqrt{a}-3)+4\geq 0$, то есть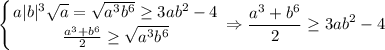 $$\left \{ {{a|b|^3\sqrt{a}=\sqrt{a^3b^6}\geq 3ab^2-4} \atop {\frac{a^3+b^6}{2}\geq \sqrt{a^3b^6} }} \right. \Rightarrow \frac{a^3+b^6}{2} \geq 3ab^2-4$

Что и требовалось доказать (естественно, неравенство справедливо по условию с ограничением a>0)