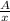и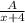 
соответственно. С другой стороны, можно найти их общую производительность, зная время совместной работы экскаваторов
.
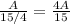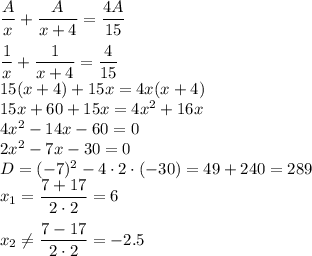
Уравнение четвертой степени имеет максимум 4 корня.
Если все они действительные - то согласно правилу знаков Декарта - все они положительные , так как знак коэффициентов меняется 4 раза. ( + - + - + )
Согласно теореме Виетта сумма корней уравнения n - степени равна частному от деления коэффициента при степени n-1 на коэффициент при n - степени с противоположным знаком .
В нашем случае это 26/1 = 26
Определим точки перегиба функции в левой части Уравнения
f"(x) = (x^4-26x^3+160x^2-100x+7)" = 12x^2 - 156x +320
f"(x) =0
12x^2 - 156x +320 =0
x12 = 13/2 +- √561 / 6
x1 ≅ 2.5
x2≅10.4
- Точки перегиба
Все Корни уравнения положительные .
f(0) >0
f(2,5) >0
посмотрим есть ли на интервале от 0 до 2.5 отрицательные значения функции и соответственно 2 корня
f(0,5) = (0.5)^4-26*(0.5)^3+160*(0.5)^2-100*(0.5)+7 = -6.1875
Есть 2 действительных корня .
Посмотрим значение функции за второй точкой перегиба
f(12)= (12)^4-26*(12)^3+160*(12)^2-100*(12)+7 = -2345
При больших X - значение функции положительно ( так коэффициент при 4 степени положительный )
Значит уравнение имеет 4 действительных корня и их сумма по теореме Виетта равна 26
Т.к. переменная х в функции везде используется в квадрате, то функция будет иметь одинаковые значения в точках х2 и х3, причем положительное. При х = 0, функция примет значение 0, а в двух других критических точках значение будет больше нуля, т.е. х = 0 - точка минимума. Оставшиеся 2 точки - точки максимума