Question

Найдите max и min sina+sinb+sinc если a+b+c=180°. , с доказательством!

Answer 1

$a+b+c=180^\circ\Rightarrow c = 180^\circ - a - b\\\sin a + \sin b + \sin c = \sin a + \sin b + \sin(180^\circ-a-b)=\\=\sin a + \sin b + \sin(180^\circ)\cos(a+b)-\cos(180^\circ)\sin(a+b)=\\=\sin a + \sin b + \sin (a + b)=2\sin({a+b\over 2})\cos({a-b\over2})+\sin(a+b)=\\=2\sin({a+b\over2})(\cos({a-b\over2})+\cos({a+b\over2}))=4\sin({a+b\over2})\cos({a\over2})\cos({b\over2})$
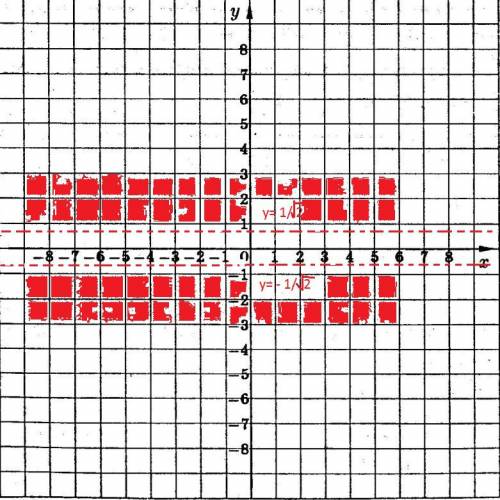
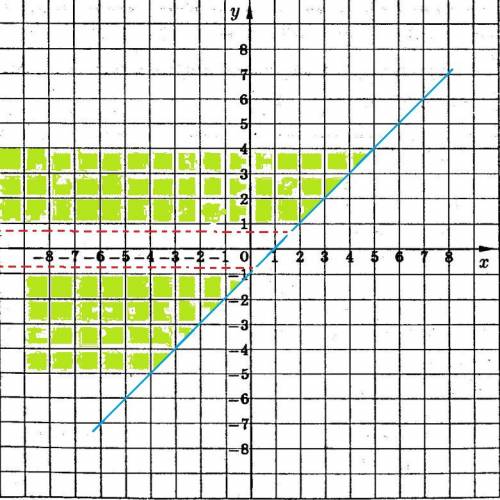
Нам достаточно найти максимум при некоторых значениях $a_1,\,b_1$, а минимум будет иметь то же по модулю значения, но обратный знак (если есть некоторое максимальное значение при $a_1,\,b_1$, то взяв $-a_1,\,-b_1$ мы получим, что синус поменяет знак на противоположный, а косинусы сохранят знак. Если же у минимума модуль больше, чем у максимума, то также поменяем знак и получим новый максимум)
Теперь осталось найти максимум.

$\sin(a)+\sin(b)+\sin(c)=2\sin({a+b\over2})\cos({a-b\over2})+\sin c\leq\\\leq2\sin({a+b\over2})+\sin(c)=2\cos({c\over2})+\sin c$
Найдем наибольшее значение функции $f(x)=2\cos({x\over2})+\sin x$:
$f'(x)=-\sin({x\over2})+\cos x\\f'(x)\ \textless \ 0\Rightarrow 1-2\sin^2{x\over2}-\sin{x\over2}\ \textless \ 0\\\sin ({x\over2})=t,\,|t|\leq1\\2t^2+t-1\ \textgreater \ 0\\2(t-{1\over2})(t+1)\ \textgreater \ 0\\t\in({1\over2};1)\Rightarrow {x\over2}\in({\pi\over6}+2\pi k;{5\pi\over6}+2\pi k),\,k\in\mathbb{Z}\\x\in({\pi\over3}+4\pi k;{5\pi\over3}+4\pi k),\,k\in\mathbb{Z}$
На полученном интервале f(x) убывает. Кроме того, f(x) имеет период 4π.
Таким же образом приходим к интервалу на котором f(x) возрастает (просто меняем знак неравенства):
$|t|\leq1\\2(t-{1\over2})(t+1)\ \textless \ 0\\t\in(-1;{1\over2})\Rightarrow {x\over2}\in(-{7\pi\over6}+2\pi k;{\pi\over6}+2\pi k),\,k\in\mathbb{Z}\\x\in(-{7\pi\over3}+4\pi k;{\pi\over3}+4\pi k),\,k\in\mathbb{Z}$
Значит достаточно проверить значение в точках 
$x={\pi\over3}+4\pi k,k\in\mathbb{Z}$
Как нетрудно убедится, в этих точках
$f(x)={3\sqrt3\over2}$
Таким образом,
$\sin a+\sin b+\sin c\leq{3\sqrt3\over2}$
Но при $a=b=c=60^\circ$ достигается это значение.

Значит максимальное значение: ${3\sqrt3\over2}$
Минимальное: $-{3\sqrt3\over2}$