А - попадание первого баскетболиста
В - попадание второго баскетболиста.
Имеем три случая
1) Если у первого баскетболиста три попадания, а у второго меньше 3 попадания
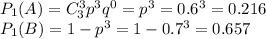
Вероятность того, что у первого баскетболиста три попадания,а у второго меньше трех попадания, равна 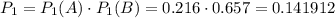
2) Если у первого баскетболиста 2 попадания, а у второго 0 или 1.
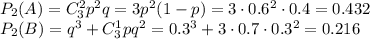
По теореме умножения, вероятность того, что первый баскетболист попадет 2 раза, а второй - 0 или 1, равна 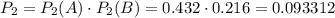
3) Если у первого баскетболиста одно попадание, то у второго 0 попаданий
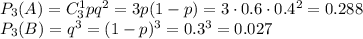
Вероятность того, что первый попадет один раз, а второй ниразу, равна
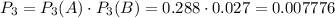
По теореме сложения, вероятность того, что у первого баскетболиста будет больше попаданий, чем у второго, равна
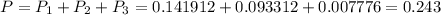
ответ: 0,243.
Формулировка и доказательство теоремы косинусов
Теорема косинусов является обобщением теоремы Пифагора для произвольного треугольника.
Формулировка теоремы косинусов
Для плоского треугольника со сторонами a,b,c и углом α, противолежащим стороне a, справедливо соотношение:
Теорема косинусов
Изображение для пояснения сути теоремы косинусов - квадрат стороны произвольного треугольника равен сумме квадратов двух других сторон минус удвоенное их произведение на косинус угла между ними
Квадрат одной стороны треугольника равен сумме квадратов двух других сторон за вычетом удвоенного их произведения, умноженного на косинус угла между ними
Полезные формулы теоремы косинусов:
Полезные формулы теоремы косинусов - сама теорема, нахождение косинуса угла по трем сторонам и нахождение самого угла по трем сторонам треугольника
Как видно из указанного выше, с теоремы косинусов можно найти не только сторону треугольника по двум сторонам и углу между ними, можно, зная размеры всех сторон треугольника, определить косинусы всех углов, а также вычислить величину любого угла треугольника. Вычисление любого угла треугольника по его сторонам является следствием преобразования формулы теоремы косинусов.
Доказательство теоремы косинусов
Теорема Косинусов
Рассмотрим произвольный треугольник ABC. Предположим, что нам известна величина стороны AC (она равна некому числу b), величина стороны AB (она равна некому числу c) и угол между этими сторонами, величина которого равна α. Найдем величину стороны BC (обозначив ее длину через переменную a)
Для доказательства теоремы косинусов проведем дополнительные построения. Из вершины C на сторону AB опустим высоту CD.
Найдем длину стороны AB. Как видно из рисунка, в результате дополнительного построения можно сказать, что
AB = AD + BD
Найдем длину отрезка AD. Исходя из того, что треугольник ADC является прямоугольным, нам известны длина его гипотенузы (b) и угол (α) то величину стороны AD можно найти из соотношения его сторон, пользуясь свойствами тригонометрических функций в прямоугольном треугольнике:
AD / AC = cos α
откуда
AD = AC cos α
AD = b cos α
Длину стороны BD найдем как разность AB и AD:
BD = AB - AD
BD = c − b cos α
Теперь запишем теорему Пифагора для двух прямоугольных треугольников ADC и BDC:
для треугольника BDC
CD2 + BD2 = BC2
для треугольника ADC
CD2 + AD2 = AC2
Обратим внимание на то, что оба треугольника имеют общую сторону - CD. Определим ее длину для каждого треугольника - вынесем ее значение в левую часть выражения, а остальное - в правую.
CD2 = BC2 - BD2
CD2 = AC2 - AD2
Поскольку левые части уравнений (квадрат стороны CD) равны, то приравняем правые части уравнений:
BC2 - BD2 = AC2 - AD2
Исходя из сделанных ранее вычислений, мы уже знаем что:
AD = b cos α
BD = c − b cos α
AC = b (по условию)
А значение стороны BC обозначим как a.
BC = a
(Именно его нам и нужно найти)
Получим:
BC2 - BD2 = AC2 - AD2
Заменим буквенные обозначения сторон на результаты наших вычислений
a2 - ( c − b cos α )2 = b2 - ( b cos α )2
перенесем неизвестное значение (а) на левую сторону, а остальные части уравнения - на правую
a2 = ( c − b cos α )2 + b2 - ( b cos α )2
раскроем скобки
a2 = b2 + c 2 - 2c b cos α + ( b cos α )2 - ( b cos α )2
получаем
a2 = b2 + c 2 - 2bc cos α
Теорема косинусов доказана.
Случай, когда один из углов при основании тупой (и высота падает на продолжение основания), полностью аналогичен рассмотренному.
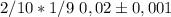
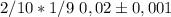
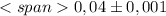
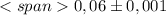
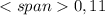
Событие - 3 броска - независимые и, поэтому вероятности для каждого участника вычисляем по формуле:
P(A) = (p+q)³ = p³ + 3p²q + 3pq² + q³. p+q = 1.
Словами это будет как - три попадания ИЛИ 3 раза два попадания и один пром ах ИЛИ з раза одно попадание и два промаха ИЛИ три промаха.
Для первого спортсмена: p =0.6, q = 1-p = 0.4. ВАЖНО: все три промаха не учитываем.
P1(A) = 0.2166 + 0.432 + 0.288 + 0,064 - первый за 3 броска.
P2(A) = 0.343 + 0.441 + 0.189 +0,027 = 0.973 - второй за 3 броска.
Вероятность, что у первого будет больше попаданий запишем как сумму вероятностей событий (запишем в виде счета)
Р(1>2) = Р(3:2)+Р(3:1)+Р(3:0)+Р(2:1)+Р(2:0)+Р(1:0) =
= Р(3)*[Р(2)+Р(1)+Р(0)] + P(2)*[P(1)]+P(0)] + Р(1)*Р(0) =
= 0.2166*(0.441+0.189+0.027) + 0.432*(0.189+0.027) + 0.288*0.027 =
= 0.1423062 + 0.093312 + 0.00778 = 0.24333942 ≈ 0.243 - ОТВЕТ