Задачка интересная, смотри, как такие решаются.
В таких задачках главное- последняя цифра числа, которое возводится в степень
В первом случае 2001 оканчивается на 1, а 1 в любой степени 1, поэтому и 2001 в любой степени оканчивается на 1.
Во втором случае число оканчивается на 9. Исследуем, на какую цифру будут оканчиваться степени 9
Степень Последняя цифра 9^n
1 9
2 1
3 9
4 1
и т.д. уже видно, что при возведении в чётную степень последняя цифра 1, в нечётную - 2
. Таким образом
1999^2002 оканчивается на 1 (2002 - чётное число)
1999^1333 оканчивается на 2 (1333 - нечётное число).
Вот, примерно, так.
Попробуй исследовать поведение последней цифры числа 2013^n, 1917^n. Получится интересней.
Ну и последнее. Всё это просто рассуждения, а как же это всё доказать, можешь ты спросить. Так же просто. Смотри, например, случай 1.
Любое число, оканчивающееся на 1 можно представить в виде 10*к +1. Значит его степень
(10*к+1)^n = 10^n*k^n + +1^n(это бином Ньютона) = 10*R +1.
то есть любое число, оканчивающееся на 1 в любой степени оканчивается на 1.
Так же через бином Ньютона доказывается и всё остальное.
Успехов!
Да, и ещё. Условие у тебя очень нечёткое, если в самом деле нет запятых, то в 1 - решение то же, а в 2 нужно поисследовать ещё на какую цифру оканчивются степени 2002, то есть 2
степень посл. цифра 2^n
1 2
2 4
3 8
4 6
5 2
6 4
7 8
ну и тд. то есть это всегда чётное число, поэтому
(1999)^(2002^1333) оканчивается на 1, так как показатель чётный.
Вот теперь совсем всё.
Пиши четче задания! Видишь, как много может значить какая-то запятая!
Ну мы знаем формулу суммы арифметической прогресси вида
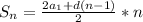
У нас же с данным значением найти сумму 11 она будет выглядеть так
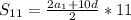
Сл-но для нас надо найти главное значение вверху дроби.Я сделала так
Представим а1+а4+а13 =-27 так а1+а1+3d+а1+12d=-27
Выносим общий множитель
3(а1+5d)=-27
а1+5d=-9
Теперь полученное значение а1+5d=-9 прибавляем к сумме 3а1+15d=-27 и у нас получается
4a1+20d=-36 Можно сказать вот мы и нашли то чт нам нужно.Делим получившееся выражения на 2
4a1+20d=-36 | :2
2a1+10d=-18 Вот что мы и искали.Ну атеперь нам лего найти сумму
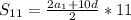
В эту формулу подставляем найденные значения и получаем
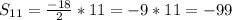
На самом деле задача сложная.Очень трудно понять что надо именно в ней искать