Ивану Царевичу нужно загадать 15552. Каждый день он будет делить это число на натуральное, превосходящее 1. Лучше всего делить на 2, но 2 дня подряд нельзя использовать одно и то же число, поэтому на второй день он поделит то, что получилось, на 3. На третий день снова на 2 и так далее. Чередование 2 и 3.
Делим:
15552/2=7776 (первый день);
7776/3=2592 (второй день);
2592/2=1296 (третий день);
1296/3=432 (четвёртый день);
432/2=216 (пятый день);
216/3=72 (шестой день);
72/2=36 (седьмой день);
36/3=12 (восьмой день);
12/2=6 (девятый день);
6/3=2 (десятый день);
2/2=1 (одиннадцатый день, в который его съедят).
Итак, загадав 15552, Иван Царевич сможет продержаться ещё 10 дней.
Чтобы получить это число, необходимо понимать, что в конце концов мы придём к 1. Поэтому 15552 мы получим следущий образом:
1•2•3•2•3•2•3•2•3•2•3•2 (6 умножений на 2 и 5 умножений на 3).
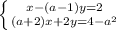
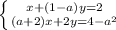
Система эквивалентных уравнений имеет бесконечное количество решений, это означает, что отношения коэффициентов при неизвестных и свободных членов должны быть равны.
отношения коэффициентов при 
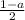отношения коэффициентов при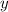 
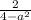отношения свободных членов
Получаем равенство.
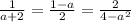
Решаем попарно.
1) Равенство первой и второй дробей
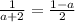
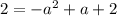
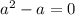
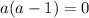
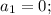
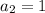
2) Равенство первой и третьей дробей
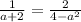
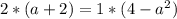
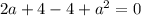
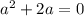
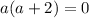
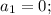
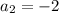
3) Равенство второй и третьей.
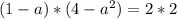
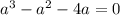
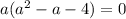
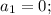
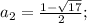
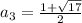
Общее решение: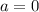 
ответ: при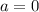
y=(lnx).x³
u=lnx, v=x³
y´=1/x .x³ + (lnx).3x²=x²+3x²lnx=x²(1+3lnx)
x=3: y´(3)=3²(1+3ln3)=9(1+ln(3³)=9(1+ln27)