Такого значения параметра
b не существует.
Объяснение:
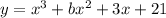
Находим производную
у'=

Приравниваем производную 0:
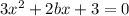
функция только убывает, если
на всей области определения
у'<0.
==>
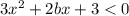
Рассмотрим уравнение:
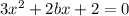
Это уравнение квадратичной
функции. Старший коэффици
ент а=3>0 ==>
если представить ее график
- это парабола, ветви которой
напрвлены вверх (парабола не
может полностью находиться
под осью абсцисс, так
как ее ветви бесконечно про
должаются вверх).
Вывод:
Условие у'<0 невыполнимо.
==> не существует такого зна
чения параметра b, когда функ
ция
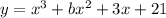
убывает на всей области оп
ределения.
Объяснение:
О - точка пересечения диагоналей ВD и АС. ВО/OD=2/5. h=BC=4
1) Тр-ки ВОС и AOD подобны по трем соответственно равным углам (1 пара вертикальных и 2 пары накрест лежащих). Из подобия следует пропорциональность сходственных сторон: BC/AD=BO/OD; AD=BC*OD/BO=4*5/2=10.
2) Проведем две высоты ВN и СМ. Высоты разделят нижнее основание на отрезки;
NM=BC=4; AN=MD=(AD-NM)/2=3.
3) Тр-к ABN с катетами BN=4 и AN=3 - египетский. Значит, гипотенуза АВ=5. (А можно найти АВ по теореме Пифагора),
4) Р=2*АВ+BC+AD=10+4+10=24 см.
x-длина
x-2 ширина
1) P=2(x+x-2)=2(2x-2)=4(x-1)
2)Y=P
Y=4x-4 - линейная функция вида y=kx+b, где k=4; b=4
3)Область определения функции, x лежит в промежутке (0;+бесконечность)
4) x=5, y=4*5-4=20-4=16
x=10, y=4*10-4=40-4=36
x=14, y=4*14-4=56-4=52
x=16, y=4*16-4=64-4=60
5) Область значений функции y лежит в промежутке (0;+бесконечность)