Решить 1.-10х-6(-1+6х)=-4х-8 2.9х-7(-10-3х)=х+3 3.2х-2(-3-10х)=-4х-4 4.-8х-4(-5+9х)=-5х-9 5.-10х-7(9-8х)=-х-2

👇

Ответ:

lourln

08.04.2023

Понравился ответ? Поставь его лучшим!
(и кстати в 5 получается 62/47)
Решить 1.-10х-6(-1+6х)=-4х-8 2.9х-7(-10-3х)=х+3 3.2х-2(-3-10х)=-4х-4 4.-8х-4(-5+9х)=-5х-9 5.-10х-7(9

4,7(62 оценок)

Открыть все ответы

Ответ:

lands4552

08.04.2023

Объяснение:

ВАРИАНТ 1.

Задание 1) у= х^2

Подставляем значения х и у в данную фунцкию:

A( 3:-9) , Где х=3, у= -9 (и последующие точки по аналогии)

Подставляем: -9=3^2

-9=9 - неверно, зн. точка не принадлежит графику функции у= х^2

B( 1;1)

у= х^2

1=1^2

1=1- верно, зн. точка принадлежит графику функции у= х^2

C(-1;-1)

у= х^2

-1=1 - неверно, зн. точка не принадлежит графику функции у= х^2

D ( -3;9)

у= х^2

9= 9 - верно, зн. точка принадлежит графику функции у= х^2

Задание 2)

а) х (нулевое) = -b\2a = 4\2= 2

у (нулевое) = у(х)=у(2) = 4-8+5= 1

(2;1)-вершина

б) х(нулевое) = 7\4

у(нулевое) = 2*49\16 - 7*7\4 + 9 = 49\8 - 49\4 + 9 = 49\8 - 96\8 +9 = = -49\8 + 9= 9 - 6 1\8 = 8 8\8 - 6 1\8 = 2 7\8

( 7\4; 2 7\8) - вершина

Задание 3.)

1) Пусть у = 0, тогда -2х^2 + 3х +2 = 0

D= 25

х 1 =- 1\2 х2 = 2

( -1\2 ;0) , (2;0) - точки пересечения параболы с осью ОХ

Пусть х=0 , тогда y=2

(0;2) - точка пересечения параболы с осью OY

4) у = х^2 - 2х -1

а) х (нулевое) = 2\2= 1

у(нулевое) = 1-2-1= -2

(1;-2) - вершина параболы

б) Пусть х=0, тогда у= -1

(0;-1) - точка пересечения с осью ОУ

в) х= -1, 2 ,3(подставляем значения х)

у= 2, -5, -4

Далее строим параболу по этим точкам. Находим, где функция возрастает, а где убывает.

4,5(83 оценок)

Ответ:

STavctva

08.04.2023

1) y=sin x, y=cos x, x=-5π/4, x=π/4.
Заданный отрезок графиками функций разбивается на 2 участка: левая часть - от заданного предела x=-5π/4 до точки встречи графиков, где график функции синуса выше графика косинуса.
Направо от этой точки график синуса выше графика косинуса.
Это определяет площадь как сумма интегралов разностей функций.
Точка встречи - это значение (-π+(π/4)) = -3π/4.
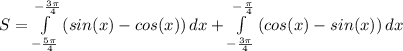$S= \int\limits^{- \frac{3 \pi }{4} }_{- \frac{5 \pi }{4} } {(sin(x)-cos(x))} \, dx + \int\limits^{- \frac{ \pi }{4} }_{- \frac{3 \pi }{4} } {(cos(x)-sin(x))} \, dx$ .
Значения аргумента в заданных пределах:
-1.25π = -3.92699,
-0.75π = -2.35619,
0.25π = 0.785398.
Значения функции синуса в заданных пределах:
0.707107, -0.70711, 0.707107. (это +-√2/2)
Значения функции косинуса в заданных пределах:
-0.70711, -0.70711, 0.707107. (это +-√2/2)
Значения функции косинуса в заданных пределах:
Площадь равна 1.414214 + 2.828427 = 4.242641 = 3√2.

2) y=-x^2-2x+4, y=-x^2+4x+1, y=5.
Заданный отрезок графиками функций разбивается на 2 участка, граничные точки которых надо определить.
Средняя точка - равенство функций y=-x^2-2x+4, y=-x^2+4x+1.
-x^2 - 2x + 4 = -x^2 + 4x + 1,
6х = 3,
х = 3/6 = 1/2.
Левая точка - равенство y=-x^2-2x+4, y=5
-x^2 - 2x + 4 = 5.
-x^2 - 2x -1 = 0.
Квадратное уравнение, решаем относительно x: Ищем дискриминант:
D=(-2)^2-4*(-1)*(-1)=4-4*(-1)*(-1)=4-(-4)*(-1)=4-(-4*(-1))=4-(-(-4))=4-4=0; Дискриминант равен 0, уравнение имеет 1 корень:
x=-(-2/(2*(-1)))=-(-2/(-2))=-(-(-2/2))=-(-(-1))=-1.
Правая точка - равенство y=-x^2+4x+1, y=5.
-x^2 + 4x + 1 = 5.
-x^2 + 4x - 4 = 0.
Квадратное уравнение, решаем относительно x: Ищем дискриминант:
D=4^2-4*(-1)*(-4)=16-4*(-1)*(-4)=16-(-4)*(-4)=16-(-4*(-4))=16-(-(-4*4))=16-(-(-16))=16-16=0; Дискриминант равен 0, уравнение имеет 1 корень:
x=-4/(2*(-1))=-4/(-2)=-(-4/2)=-(-2)=2. Линия у = 5 находится выше парабол.
Площадь равна:
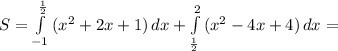
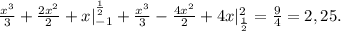
$S= \int\limits^{ \frac{1}{2} }_{-1} {(x^2+2x+1)} \, dx + \int\limits^2_{ \frac{1}{2} } {(x^2-4x+4)} \, dx =$ $\frac{x^3}{3}+ \frac{2x^2}{2}+x|_{-1}^{ \frac{1}{2} }+ \frac{x^3}{3}- \frac{4x^2}{2}+4x|_{ \frac{1}{2} }^2= \frac{9}{4}=2,25.$