logo
Вход Регистрация Спроси Mozg AI
М
Молодежь
К
Компьютеры-и-электроника
Д
Дом-и-сад
С
Стиль-и-уход-за-собой
П
Праздники-и-традиции
Т
Транспорт
П
Путешествия
С
Семейная-жизнь
Ф
Философия-и-религия
Б
Без категории
М
Мир-работы
Х
Хобби-и-рукоделие
И
Искусство-и-развлечения
В
Взаимоотношения
З
Здоровье
К
Кулинария-и-гостеприимство
Ф
Финансы-и-бизнес
П
Питомцы-и-животные
О
Образование
О
Образование-и-коммуникации
fghjik
fghjik
28.05.2022 21:01 •  Алгебра

Найдите наименьшее двухзначное число,которое является делителем для выражения 27^3+18^3: 567 85

👇
Увидеть ответ
Ответ:
АааLoo
АааLoo
28.05.2022
Вот, посмотри на этой фотографии. вдруг

Найдите наименьшее двухзначное число,которое является делителем для выражения 27^3+18^3: 567 85
4,4(61 оценок)
Ответ:
этояученик
31(в кубе) - 13(в кубе) /511 = 54 это раз
54 = 13*2*2 это два
значит получается, что 54 можно поделить на: 2, 4, 13, 26 это три
ОТВЕТ: 13 
Как кто так хотя я посмотрела уже есть такой ответ:(
4,8(83 оценок)
Открыть все ответы
Ответ:
Qwerty23459484
Qwerty23459484
28.05.2022

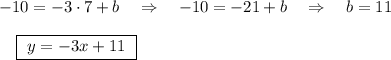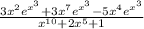
\frac{3x^{2}e^{x^{3}}+3x^{7}e^{x^{3}}-5x^{4}e^{x^{3}}}{x^{10}+2x^{5}+1}

Объяснение:

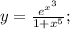
y=\frac{e^{x^{3}}}{1+x^{5}};

Производная дроби находится по следующей формуле:

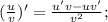
(\frac{u}{v})'=\frac{u'v-uv'}{v^{2}};

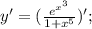
y'=(\frac{e^{x^{3}}}{1+x^{5}})';

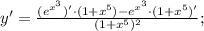
y'=\frac{(e^{x^{3}})' \cdot (1+x^{5})-e^{x^{3}} \cdot (1+x^{5})'}{(1+x^{5})^{2}};

Функция

e^{x^{3}}

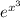
является сложной функцией. Производная сложной функции находится по следующей формуле:

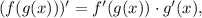
(f(g(x)))'=f'(g(x)) \cdot g'(x),

отсюда получаем

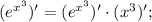
(e^{x^{3}})'=(e^{x^{3}})' \cdot (x^{3})';

Если ввести замену

t=x^{3},

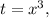
то выражение

e^{x^{3}}

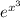
преобразуется как

e^{t}.

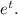
Производная последнего выражения является табличным значением:

(e^{t})'=e^{t};

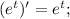
Возвращаясь к замене, получаем:

e^{x^{3}}.

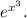
Производная второго множителя находится по следующей формуле:

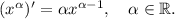
(x^{\alpha})'=\alpha x^{\alpha-1}, \quad \alpha \in \mathbb {R}.

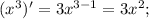
(x^{3})'=3x^{3-1}=3x^{2};

Подставим полученные значения в произведение:

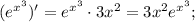
(e^{x^{3}})'=e^{x^{3}} \cdot 3x^{2}=3x^{2}e^{x^{3}};

Подставим значение этой производной в дробь:

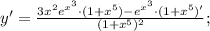
y'=\frac{3x^{2}e^{x^{3}} \cdot (1+x^{5})-e^{x^{3}} \cdot (1+x^{5})'}{(1+x^{5})^{2}};

Производная суммы равна сумме производных:

(u+v)'=u'+v';

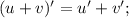
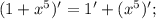
(1+x^{5})'=1'+(x^{5})';

1 — константа. Производная константы равна нулю.

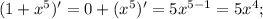
(1+x^{5})'=0+(x^{5})'=5x^{5-1}=5x^{4};

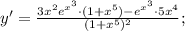
y'=\frac{3x^{2}e^{x^{3}} \cdot (1+x^{5})-e^{x^{3}} \cdot 5x^{4}}{(1+x^{5})^{2}};

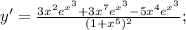
y'=\frac{3x^{2}e^{x^{3}}+3x^{7}e^{x^{3}}-5x^{4}e^{x^{3}}}{(1+x^{5})^{2}};

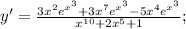
y'=\frac{3x^{2}e^{x^{3}}+3x^{7}e^{x^{3}}-5x^{4}e^{x^{3}}}{x^{10}+2x^{5}+1};

4,7(55 оценок)
Ответ:
kilaur
kilaur
28.05.2022

ответ:   y= -3x+11  .

Уравнение функции, описывающей прямо пропорциональную зависимость между переменнными "х" и "у" , такая:   y=kx  .

Подставим координаты точки А(-4;12) в это равенство и найдём коэффициент  k  .

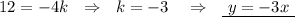
 12=-4k\ \ \Rightarrow \ \ k=-3\ \ \ \Rightarrow \ \ \underline {\ y=-3x\ }

Линейная функция задаётся уравнением 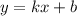 y=kx+b  .  

Так как график линейной функции параллелен графику прямой пропорциональности, то у этих функций будут равные угловые коэффициенты, то есть линейная функция будет иметь вид 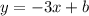 y=-3x+b

 Найдём число  "b"  , подставив координаты точки D(7;-10)  в уравнение линейной функции.

 -10=-3\cdot 7+b\ \ \ \Rightarrow \ \ \ -10=-21+b\ \ \ \Rightarrow \ \ \ b=11\\\\{}\ \ \ \boxed {\ y=-3x+11\ }

4,4(93 оценок)
Это интересно:
В
Как сохранить романтику: секреты успешных отношений...
К
Запекись, стейк! Как подогреть мясо и не испортить его вкус...
К
Как приготовить легкие и сочные вегетарианские блинчики в домашних условиях...
И
Как правильно выбрать гитарный усилитель для рок музыки...
К
Как тушить ароматные овощи: 5 шагов к вкусному ужину...
К
Невероятные способы приготовления крабовых ножек: шаг за шагом...
В
Как относиться к мужчине, чтобы он не изменял...
Д
Дом-и-сад
19.01.2023
Орхидеи: как выбрать этот красивый цветок...
К
Как настроить Outlook 2007 для работы с Gmail...
З
Здоровье
23.07.2022
Шина при повреждении разгибательного аппарата на уровне дистального межфалангового сустава: эффективность лечения...
Новые ответы от MOGZ: Алгебра
хорошист549
хорошист549
22.05.2021
1. Функцію задано формулою g(x) 2 - x 2+x Знайдіть: 1) g(-1); 2) таке значення при якому g(x) = -5...
ChaffaYT
ChaffaYT
23.07.2020
Решите уравнение x^2 + 8x + 15 = 0...
alishertursunov
alishertursunov
08.03.2023
Найдите неизвестные член пропоруци 45/30=x/6...
cucheryavy
cucheryavy
26.02.2021
Раскрой скобки и упрости выражение: −9(5−a)+2(−3a−3)−6(−9+a)...
motorindmitry12
motorindmitry12
14.05.2023
РЕШИТЕ ПРИМЕР ПО АЛГЕБРЕ 1.14...
fedarmo
fedarmo
09.02.2020
Упростите выражение 2y^6 : 4y^4...
jfksbsj
jfksbsj
26.07.2020
Даны функции: f (x) = x” – 2х и g (x) = 2х – 4. Найдите: а)f(-1); g(-4); f (g (-2)). б) Значения аргументах, при которых g(x) = 3....
reor1878p02hjw
reor1878p02hjw
26.07.2020
Задания к таблице Определите степень полученных уравнений Среди полученных уравнений укажите нелинейные Почему их называют нелинейными? Все ли уравнения определяют функциональную...
mspasenkova
mspasenkova
30.06.2022
Сделайте задание по математике...
Katyag2000
Katyag2000
13.04.2023
1.35. Запишите произведение вв. 1) n12.n°; 7/7 4) а-а”; 2) т°.m17, 5) a16. а”; 3) с.с, - 6) p10.p ; 7) b.b-b2; 8) х? . х. х3; 9) r?.r2.r2. – TT TO om...

MOGZ ответил

Полный доступ к MOGZ
Живи умнее Безлимитный доступ к MOGZ Оформи подписку
О НАС
ПОМОЩЬ
App
.
.
logo
Вход Регистрация
Что ты хочешь узнать?
Спроси Mozg
Открыть лучший ответ