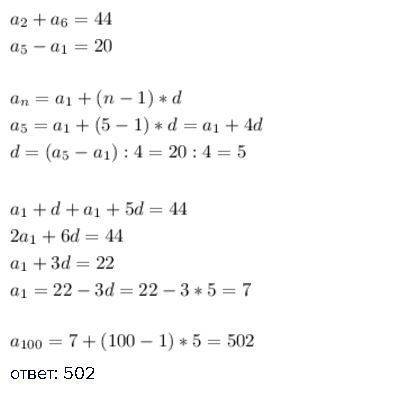
y=-x^2+6x-4
1) графиком является парабола , оси направлены вниз, так как перед х2 коэффициент отрицательный
2) точки пересечения с ОХ
-х2+6х-4=0
Д=20 или 2 корня из 5
6+2корня из 5 2(3+корень из 5) (3+корень из 5)
х===
4 4 2
х= (3-корень из 5) делить на 2
эти 2 значения х будут точки пересечения с ОХ
(3-корень из 5) делить на 2 ;0) и вторая аналогично
с ОY
подставляем под х о будет (0,-4)
3) вершина
Х0=-В/2А=-6/-2=3
Y0(3)=-9+18-4=5
вершина (3;5)
вот теперь отмечаешь все эти точки , вот тебе и график, при этом не забываешь, что оси вниз, еще 3-корень из 5 равно примерно 0.8, 3+корень из 5 =5.2
1. При каких значениях а уравнение sin ^2 x - (a+3) sin x + 3a = 0 не имеет решений ?
2. Решите уравнение cos ^2 x + cos 4x = a , если одно из его решений п/3
Участник Знаний
1. Квадратное уравнение не имеет решений, если его дискриминант отрицателен.
\sin^2x-(a+3)\sin x+3a=0\\\sin x=t,\;\sin^2x=t^2,\;-1\leq t\leq1\\t^2-(a+3)t+3a=0\\D=(-(a+3))^2-4\cdot1\cdot3a=(a+3)^2-12a=a^2-6a+9=(a-3)^2\\(a-3)^2
Последнее неравенство не имеет решений. Значит, исходное уравнение имеет решение (-ия) при любых а.
2.\;\cos^2x+\cos4x=a\\\cos4x=8\cos^4x-8\cos^2x+1\\\cos^2x+8\cos^4x-8\cos^2x+1=a\\8\cos^4x-7\cos^2x+(1-a)=0\\\cos^2x=t,\cos^4x=t^2,\;0\leq t\leq1\\8t^2-7t+(1-a)=0\\D=49-4\cdot8\cdot(1-a)=49-32+32a=17+32a\\t_{1,2}=\frac{7\pm\sqrt{17+32a}}{16}
Один из корней п/3, значит x=\frac\pi3\Rightarrow\cos x=\frac12\Rightarrow\cos^2x=t=\frac14
\frac{7\pm\sqrt{17+32a}}{16}=\frac14\Rightarrow\begin{cases}\frac{7+\sqrt{17+32a}}{16}=\frac14\\\frac{7-\sqrt{17+32a}}{16}=\frac14\end{cases}\Rightarrow\begin{cases}{7+\sqrt{17+32a}}=4\\{7-\sqrt{17+32a}}=4\end{cases}\Rightarrow\\
\Rightarrow\begin{cases}\sqrt{17+32a}=-3\\\sqrt{17+32a}=3\end{cases}\Rightarrow 17+32a=9\Rightarrow32a=-8\Rightarrow a=-\frac14=-0,25\\t_1=\frac{7+\sqrt{17-32\cdot0,25}}{16}=\frac{7+\sqrt{9}}{16}=\frac{10}{16}=\frac58\\t_2=\frac{7-\sqrt{17-32\cdot0,25}}{16}=\frac{7-\sqrt{9}}{16}=\frac{4}{16}=\frac14\\\cos^2x=\frac14\Rightarrow\cos x=\frac12\Rightarrow x=\frac\pi3+2\pi n,\;n\in\mathbb{Z}\\\cos^2x=\frac58\Rightarrow\cos x=\sqrt{\frac58}\Rightarrow x=\arccos\left(\sqrt{\frac58}\right)+2\pi n,\;n\in\mathbb{Z}
Объяснение:
ответ: 502