Объяснение:
Приравняем числитель и знаменатель к нулю, тогда
x^2-3x-10=0
x^2-6x+5=0. решим эти уравнения любым удобным , для меня это теорема обратная Т.Виета
произведение корней равно минус 10, а сумма равна 3, очевидно это 5 и минус 2, произведение корней равно 5, а сумма 6, очевидно это 5 и 1, и очень хорошо, что есть одинаковые корни. Мы имеем право записать квадратный трехчлен как a(x-x1)*(x-x2), где х1 и х2 это корни квадратного трехчлена, a - коэффициент перед старшей степенью. Тогда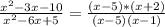
на х-5 можно сократить, окончательно получим.
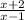
Число (-103) не является членом данной арифметической прогрессии.
Объяснение:
1) d = (a₅ - a₁) : 4 = (3 - 31) : 4 = - 28 : 4 = - 7
2) Если число (-103) является членом данной прогрессии, то разность между этим числом и пятым членом прогрессии должна быть кратна d, то есть делиться нацело на d:
а) - 103 - 3 = -106
б) 106 без остатка на 7 не делится; следовательно, число (-103) не является членом данной арифметической прогрессии.
ответ: число (-103) не является членом данной арифметической прогрессии.
3^x (1 + 3) = 4
3^x * 4 = 4
3^x = 1
3^x = 3^0
x = 0
5^(2x) - 6*5^x + 5 = 0
5^x = t ==>
t^2 - 6t + 5 = 0
D = 36 - 20 = 16
t1 = (6 + 4)/2 = 10/2 = 5
t2 = (6 - 4)/2 = 2/2 = 1
5^x = 5
x = 1
5^x =1
x = 0