Сделайте рисунок и сразу увидите решение.
В каждом из этих треугольников один угол прямой, так как высота - это перпендикуляр, а еще по одному равны как вертикальные. Следовательно, третий угол в них тоже равен.
Эти треугольники подобны по равенству их трех углов.
Если два угла одного треугольника равны двум углам другого треугольника, то такие треугольники подобны.
А прямоугольные треугольники подобны, если острый угол одного треугольника равен острому углу другого. Здесь острые углы - вертикальные и равны.
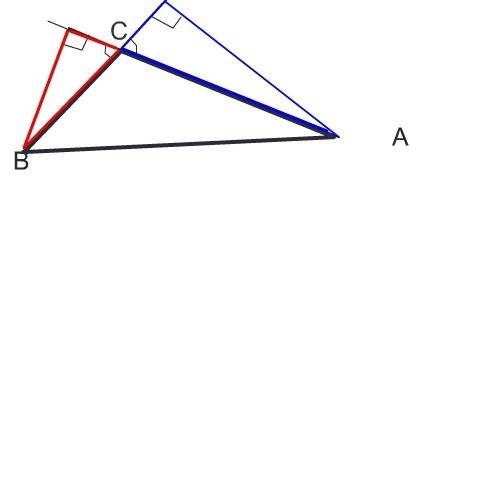
Сделайте рисунок и сразу увидите решение.
В каждом из этих треугольников один угол прямой, так как высота - это перпендикуляр, а еще по одному равны как вертикальные. Следовательно, третий угол в них тоже равен.
Эти треугольники подобны по равенству их трех углов.
Если два угла одного треугольника равны двум углам другого треугольника, то такие треугольники подобны.
А прямоугольные треугольники подобны, если острый угол одного треугольника равен острому углу другого. Здесь острые углы - вертикальные и равны.

1) А(0;0; ZA) - точка пересечения с осью аппликат OZ,
2) B(0, YB, 0) - пересечение с осью ординат OY,
3) C(XC, 0, 0) - пересечение с осью абсцисс OX.
Подставив в уравнение 3x - y + 2z - 5 = 0 условие 1) х=0, у =0, найдем 2z - 5 = 0
ZA = 5/2,
Подставив в уравнение 3x - y + 2z - 5 = 0 условие 2) х=0, z =0, найдем - y - 5 = 0
YB = - 5,
Подставив в уравнение 3x - y + 2z - 5 = 0 условие 3) z=0, у =0, найдем 3x - 5 = 0
XC = 5/3,
ОТВЕТ:
1) А(0;0; 5/2) - точка пересечения с осью аппликат OZ,
2) B(0, -5, 0) - пересечение с осью ординат OY,
3) C(5/3, 0, 0) - пересечение с осью абсцисс OX.