Примем за 1 - объем цистерны
Пусть t цис./ч - производительность "медленного" насоса.
Тогда 3t цис./ч - производительность "быстрого" насоса.
(t+3t) цис./ч - производительность системы при совместной работе этих двух насосов.
(t+3t)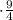
- объем работы системы из двух насосов за 2ч 15мин.
Получим уравнение: 
9t = 1
Значит,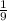 
- цис./ч - производительность "медленного" насоса.
Тогда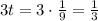 
- цис./ч - производительность "быстрого" насоса.
Следовательно,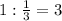 
ч - потребуется "быстрому" насосу на заполнение цистерны.
ответ: 3 ч.
(19, 342), (20, 180), (21, 126), (22, 99), (24, 72), (27, 54) и (36, 36)
Объяснение:
Представим уравнение в другом виде:
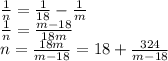
324 можно разложить на простые множители: 2²·3⁴
Значит m-18 должно содержать эти множители. Он может быть равен 1,2,3,4,6,9,18,108 и 324. Соответствующие m для этого: m = 19,20,21,22,24,27,36,126 и 342
При последовательной подстановке этих чисел в уравнении нахождения чисел n, мы получаем: n = 342, 180, 126, 99, 72, 54, 36, 21 и 19. Среди них подходят пары (19, 342), (20, 180), (21, 126), (22, 99), (24, 72), (27, 54) и (36, 36)
2) (z-3)*(1+z^2)=0 (аналогично)