1. Натуральные 100; 21; 10 (натуральные - это числа, которые возникают при счете предметов.)
Целые 100; 21; 0 ; 10; - 15; -24; (целые - это натуральные, им противоположные и нуль.)
Рациональные -3,2 ; 100; - 14,5; 21; 0; 10; - 15; 1,2333 ...=1.2(3) ; -2,121121112 т.к. можем представить в виде р/q, где р- целое, q- натуральное.
Иррациональные 5, 1313111...; 0,1010010001...; (т.к. иррациональные числа - это числа, которые в десятичной записи представляют собой бесконечные непериодические десятичные дроби).
2.а) каждое натуральное число является целым - да.
б) каждое число является натуральным. - нет.
в) каждое число является рациональным - нет.
г) каждое рациональное число является действительным - да.
д) каждое действительное число является рациональным - нет.
е) каждое иррациональное число является действительным - да.
ж) каждое действительное число является иррациональным - нет.
Задание 3.
Сравните числа. а) 7,653>7,563
б) 1,(56) > 1,56
в) - 4,(45) < -4,45
г) 1,(34) <1,345
Задание 4:
Число 7,15 г) рациональное, т.к. 7,15=715/100
Число - 35. б) целое
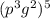·g - в одночлене должны быть записаны степени различных переменных, здесь записана степень произведения.
разница в скорости лодки и плота = 18 км/час;
расстояние встречи от пристани = 20 км
Найти: скорость плота
Решение:
Скорость движения плота равна скорости течения, примем ее за Х;
(Х + 18) скорость лодки:
20/Х , час время движения плота до встречи;
20(Х+18) , час время движения лодки до встречи;
20/Х - 20/(Х+18) = 9 т.к. по условию плот отплыл на 9 часов раньше;
Приведем к общему знаменателю Х(Х+18) и умножим на него все члены уравнения, чтобы избавиться от него.
20(Х+18) - 20Х = 9Х(Х+18)
20Х + 20*18 - 20Х = 9Х² + 9*18Х
9Х² + 9*18Х - 20*18 = 0 | : 9
Х² + 18Х - 40 = 0
D = 18²+4*40 = 484; D>0
Х₁ = (-18 +√Д)/2 = (-18+22)/2 = 2 (км/час)
Х₂ = (- 18-22)/2 = -20 не подходит, т.к. скорость течения больше 0
ответ: 2 км/час скорость движения плота
Проверка: 20/2 - 20/(2+18) = 9; 9=9
Дано: час випередження плота = 9час
різниця в швидкості човни і плоти = 18 км/год;
відстань зустрічі від пристані = 20 км
Знайти: швидкість плота
Рішення:
Швидкість руху плота дорівнює швидкості течії, приймемо за Х;
(Х + 18) швидкість човна:
20/Х , годину час руху плота до зустрічі;
20(Х+18) , годину час руху човна до зустрічі;
20/Х - 20/(Х+18) = 9 оскільки за умовою пліт відплив на 9 годин раніше;
Наведемо до спільного знаменника Х(Х+18) і помножимо на нього всі члени рівняння, щоб позбутися від нього.
20(Х+18) - 20Х = 9Х(Х+18)
20Х + 20*18 - 20Х = 9Х² +9*18Х
9Х² + 9*18Х - 20*18 = 0 | : 9
Х² + 18Х - 40 = 0
D = 18²+4*40 = 484; D>0
Х₁ = (-18 +√Д)/2 = (-18+22)/2 = 2 (км/год)
Х₂ = (- 18-22)/2 = -20 не підходить, оскільки швидкість течії більше 0
Відповідь: 2 км/год швидкість руху плота
Перевірка: 20/2 - 20/(2+18) = 9; 9=9