Раскроем модуль. (на фото) Получили кусочную функцию
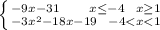
При этом наш параметр а остался в обоих выражениях:
-9х - 31 + а при х≤-4 и х≥1
-3х² - 18х - 19 + а при -4<x<1
Стоит отметить что а - свободный член, с этого следует, что параметр а отвечает за перемещение нашего графика вверх-вниз относительно оси Оу. Построим нашу кусочную функцию: (фото)
По графику функции видно, что практически на всей области определения график будет иметь 1 пересечение с горизонтальной прямой (нашей осью абсцисс),в двух точках будет иметь 2 пересечения, и на определённом участке будет иметь целых 3 нужных нам пересечения.
При а = -5 наш график переносится на 5 клеток вниз относительно оси Оу, и теперь можно с уверенностью сказать, что при а ∈ (-5;-8) график имеет с осью абсцисс ровно 3 пересечения
ответ:при a ∈ (-5 ; -8) наша функция имеет с осью Ох 3 разных пересечения
![Найдите все значения параметра «a», при каждом из которых график функции [tex]f (x)=-1,5x^2-13,5x-25](/tpl/images/1022/5455/ca24a.jpg)
![Найдите все значения параметра «a», при каждом из которых график функции [tex]f (x)=-1,5x^2-13,5x-25](/tpl/images/1022/5455/6a95a.jpg)
![Найдите все значения параметра «a», при каждом из которых график функции [tex]f (x)=-1,5x^2-13,5x-25](/tpl/images/1022/5455/eeb27.jpg)
![Найдите все значения параметра «a», при каждом из которых график функции [tex]f (x)=-1,5x^2-13,5x-25](/tpl/images/1022/5455/c7189.jpg)
Объяснение:
a6=3
2)a12=15-2*12
a12=-9