
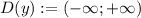
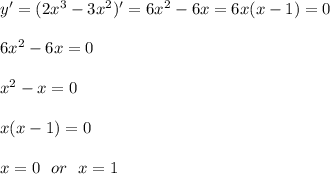
![+++++++[0]---------[1]+++++++\ \textgreater \ x](/tpl/images/0905/2672/fbfbf.png)
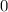 являеться максимумом функции
являеться максимумом функции 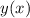 ,
, являеться минимумом функции
являеться минимумом функции 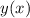
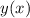 монотонно растет на промежутке
монотонно растет на промежутке 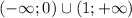
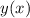 монотонно убывает на промежутке
монотонно убывает на промежутке 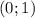
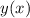 пересекает ось ОХ в точкаx
пересекает ось ОХ в точкаx 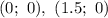
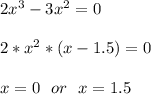
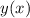 пересекает ось ОУ в точке
пересекает ось ОУ в точке 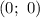
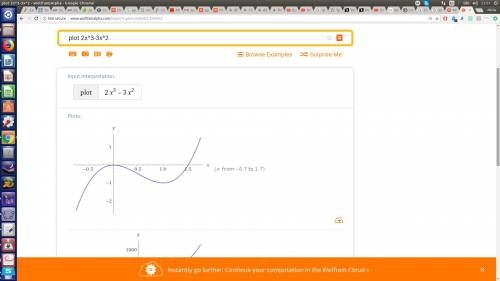
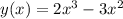
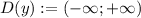
![+++++++[0]---------[1]+++++++\ \textgreater \ x](/tpl/images/0905/2664/fbfbf.png)
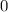 являеться максимумом функции
являеться максимумом функции 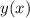 ,
, являеться минимумом функции
являеться минимумом функции 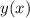
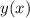 монотонно растет на промежутке
монотонно растет на промежутке 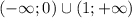
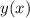 монотонно убывает на промежутке
монотонно убывает на промежутке 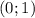
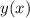 пересекает ось ОХ в точкаx
пересекает ось ОХ в точкаx 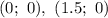
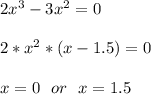
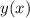 пересекает ось ОУ в точке
пересекает ось ОУ в точке 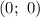
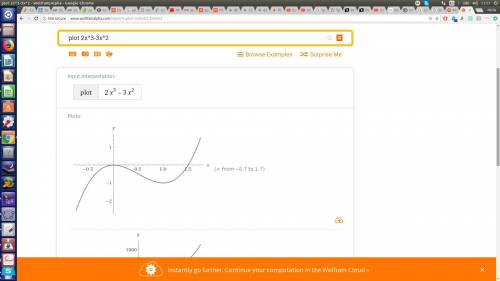
Т.к основание у логарифмов одинаковое, но основание 0< 0,3 < 1 , то поменяем знак и перейдем к следующему неравенству
Решение:
x > -4 являлось бы решением, если бы не одз, а т.к одз у нас x > 3
То решением является x > 3