Задание 1
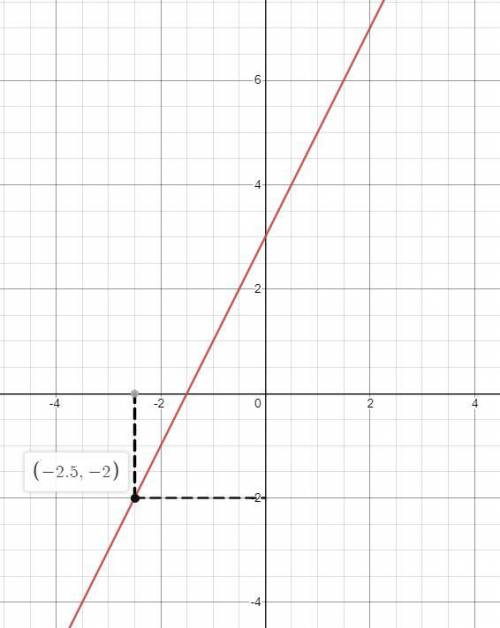
1. Строим график функции.
2. Проводим через точку x = -2.5 отрезок, перпендикулярный оси абсцисс, к графику функции.
3. Проводим через полученную точку пересечения отрезок, параллельный оси абсцисс, к оси ординат.
4. Точка пересечения этого отрезка с осью ординат и есть значение функции при заданном аргументе.
ответ: значение функции при значении аргумента -2.5 равно -2 .
Задание 2
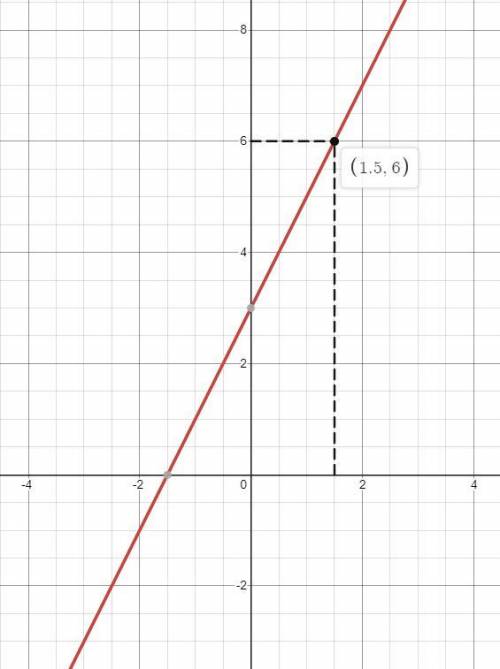
1. Строим график функции.
2. Проводим через точку y = 6 отрезок, перпендикулярный оси ординат, к графику функции.
3. Проводим через полученную точку пересечения отрезок, параллельный оси ординат, к оси абсцисс.
4. Точка пересечения этого отрезка с осью абсцисс и есть значение аргумента при заданном значении функции.
ответ: значение аргумента при значении функции 6 равно 1.5 .
Однажды в месяце Саманта шла домой с работы и увидела мужчину, который пытался ворваться в машину. Она спросила его, что он делает, и он сказал ей: «Убирайся!» Она побежала в ближайший магазин и попросила владельца вызвать полицию, что он немедленно сделал. Когда она снова вышла на улицу, то увидела, что и вор, и машина ушли. Примерно через десять минут возле магазина остановилась полицейская машина. Женщина-полицейский вышла из машины и задала Саманте несколько вопросов об инциденте. Она попросила ее описать машину и вора. Саманта сказала, что это темно-синий Mini с регистрационным номером TRO3 RMN8. Она сказала, что на правой стороне была большая царапина. Она описала мужчину как высокого с короткими темными волосами. Она сказала, что он был худощав, выглядел примерно на двадцать пять лет и был одет в синюю джинсовую куртку и черные джинсы. Полицейская все записала в блокнот. Саманта почувствовала себя немного потрясенной, но была рада, что смогла . Через несколько дней она узнала, что вор был пойман в Ньюкасле и что машина была возвращена владельцу в целости и сохранности. Прочтите отрывок и затем ответьте на следующие вопросы: 1. О ком идет этот абзац ?. 2. Когда произошел инцидент? 3. Куда она шла? 4. Что делал этот человек? 5. Что он сказал ей делать? 6. Какого цвета была машина?
1) Сделаем замену:
2. Уравнение не имеет корней тогда, когда дискриминант строго меньше нуля, а значит:
Но это ещё не всё. По хорошему, надо было бы включить случаи, когда оба корня уравнения-следствия меньше нуля, но здесь вершина параболы жёстко зафиксирована, поэтому по крайней мере один корень всегда больше нуля.
ответ: