1) 11х = 36 - х
ОДЗ уравнения:
x ∈ ( -∞, ∞)
Делаем преобразование правой части уравнения:
36 - x = - ( x - 36)
Уравнение после преобразования:
11x = - (x - 36)
Упрощаем:
12x = 36
Сокращаем:
12(убираем)x = 12(убираем) * 3
x=3
2) 9х + 4 = 48 - 2х
ОДЗ уравнения:
x ∈ ( -∞, ∞)
Делаем преобразование правой части уравнения:
48 - 2x = -2 * (x - 24)
Уравнение после преобразования:
9x + 4 = -2 * (x - 24)
Упрощаем:
11x = 44
Сокращаем:
11(убираем)x = 11(убираем) * 4
x=4
3) 8 - 4х = 2х - 16
ОДЗ уравнения:
x ∈ ( -∞, ∞)
Делаем преобразование левой части уравнения:
8 - 4x = -4 * (x - 2)
Делаем преобразование правой части уравнения:
2x - 16 = 2 * (x - 8)
Уравнение после преобразования:
-4 * (x - 2) = 2 * (x - 8)
Упрощаем:
-6x = -24
Сокращаем:
-6(убираем)x = -6(убираем) * 4
x = 4
За остальным, если желаешь - в ЛС.



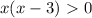
 ∈
∈ 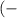 ∞
∞  ∪
∪ 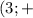 ∞
∞ 

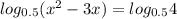
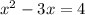
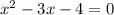
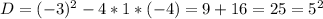
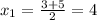
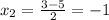


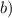

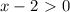
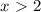
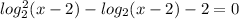

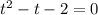

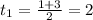

 или
или 
 или
или 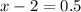
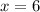 или
или 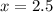

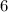
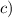
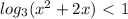

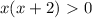
 ∈
∈ 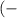 ∞
∞  ∪
∪ 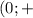 ∞
∞ 

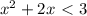


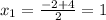

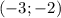 ∪
∪ 
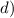
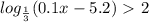







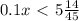



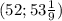
чтобы найти наименьшее значение функции, нужно сначала найти ее производную
(производная от cosx = -sinx и еще надо не забыть множитель 2)
далее нужно найти стационарные точки
это те точки, в которых производная равна нулю
следовательно приравняем нашу производную к нулю
т.к. синус не может принимать значения меньше -1, то стационарных точек нет и функция всегда возрастает или убывает
именно это мы сейчас и узнаем
для этого нужно понять, положительна ли производная или отрицательна
-2sinx имеет максимальное значение равное 2 (если синус будет равен -1, то (-2)*(-1)=2)
2-11<0, следовательно производная отрицательна и функция всегда убывает
нам нужно найти наименьшее значение на определенном промежутке [-;0]
поскольку мы выяснили, что наша функция всегда убывает, то наименьшее значение будет при наибольшем х
в нашем случае на промежутке [-;0] набольший х=0
и нам остается только лишь посчитать значение функции в нуле