Представьте в виде произведения: (a+b)^2-(a-b)^2

👇

Ответ:

texin508

17.03.2020

(a+b)²-(a-b)²= (a+b+a-b)(a+b-a+b)=2a*2b=4ab
***
Для решения применена формула разности квадратов
х²-у²=(х-у)(х+у), где х=a+b и y=a-b

4,6(48 оценок)

Открыть все ответы

Ответ:

KristinkaOvchin

17.03.2020

Пусть меньшая сторона — х метров, тогда большая — х+8 метров. Зная площадь площадки, составим и решим мат. модель:

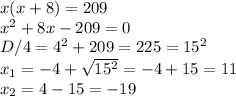
$x(x+8)=209\\x^2+8x-209=0\\D/4 =4^2+209 = 225 = 15^2\\x_1 = -4+\sqrt{15^2} = -4+15 = 11\\x_2 = 4-15=-19$

Отрицательный корень отбрасывает, т.к. длина не может быть отрицательной.

Следовательно, меньшая сторона — х = 11 метров;

большая — х+8 = 11+8 = 19 метров.

Для определения кол-ва упаковок материала для бордюра, вычислим периметр площадки:

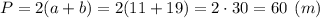
$P= 2(a+b) = 2(11+19) = 2\cdot 30 = 60 \:\: (m)$

Необходимое количество упаковок равно:

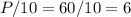
P/10 = 60/10 = 6

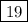Меньшая сторона детской площадки равна: $\boxed {11}$ м.Большая сторона детской площадки равна: $\boxed {19}$ м.Необходимое количество упаковок равно: $\boxed {6}$ .

4,7(28 оценок)

Ответ:

MoDnIk237

17.03.2020

Формулы для квадратов{\displaystyle (a\pm b)^{2}=a^{2}\pm 2ab+b^{2}}{\displaystyle a^{2}-b^{2}=(a+b)(a-b)}{\displaystyle \left(a+b+c\right)^{2}=a^{2}+b^{2}+c^{2}+2ab+2ac+2bc}Формулы для кубов{\displaystyle (a\pm b)^{3}=a^{3}\pm 3a^{2}b+3ab^{2}\pm b^{3}}{\displaystyle a^{3}\pm b^{3}=(a\pm b)(a^{2}\mp ab+b^{2})}{\displaystyle \left(a+b+c\right)^{3}=a^{3}+b^{3}+c^{3}+3a^{2}b+3a^{2}c+3ab^{2}+3ac^{2}+3b^{2}c+3bc^{2}+6abc}Формулы для четвёртой степени{\displaystyle (a\pm b)^{4}=a^{4}\pm 4a^{3}b+6a^{2}b^{2}\pm 4ab^{3}+b^{4}}{\displaystyle a^{4}-b^{4}=(a-b)(a+b)(a^{2}+b^{2})} (выводится из {\displaystyle a^{2}-b^{2}})Формулы для n-ой степени{\displaystyle a^{n}-b^{n}=(a-b)(a^{n-1}+a^{n-2}b+a^{n-3}b^{2}+...+a^{2}b^{n-3}+ab^{n-2}+b^{n-1})}{\displaystyle a^{2n}-b^{2n}=(a+b)(a^{2n-1}-a^{2n-2}b+a^{2n-3}b^{2}-...-a^{2}b^{2n-3}+ab^{2n-2}-b^{2n-1})}, где {\displaystyle n\in N}{\displaystyle a^{2n}-b^{2n}=(a^{n}+b^{n})(a^{n}-b^{n})}{\displaystyle a^{2n+1}+b^{2n+1}=(a+b)(a^{2n}-a^{2n-1}b+a^{2n-2}b^{2}-...+a^{2}b^{2n-2}-ab^{2n-1}+b^{2n})}, где {\displaystyle n\in N}Некоторые свойства формул{\displaystyle (a-b)^{2n}=(b-a)^{2n}}, где {\displaystyle n\in N}{\displaystyle (a-b)^{2n+1}=-(b-a)^{2n+1}}, где {\displaystyle n\in N}

4,6(48 оценок)

Это интересно:

Стиль-и-уход-за-собой

28.01.2022

Как окрасить волосы в технике Dip-Dye при помощи Kool Aid?...

Стиль-и-уход-за-собой

02.12.2022

Как создать свой неповторимый образ в стиле 80х...

Компьютеры-и-электроника

11.02.2022

Как установить новые модели машин в GTA 4: подробная инструкция...

Дом-и-сад