{ x1 + 4x2 - 7x3 + 13x4 = 0
{ 2x1 + x2 - 3x3 + 5x4 = 0
{ 3x1 - 2x2 + x3 - 3x4 = 0
{ 3x1 + 5x2 - 10x3 + 18x4 = 0
Умножаем 1 уравнение на -2 и складываем со 2 уравнением.
Умножаем 1 уравнение на -3 и складываем с 3 уравнением.
Умножаем 4 уравнение на -1 и складываем с 3 уравнением.
{ x1 + 4x2 - 7x3 + 13x4 = 0
{ 0x1 - 7x2 + 11x3 - 21x4 = 0
{ 0x1 - 14x2 + 22x3 - 42x4 = 0
{ 0x1 - 7x2 + 11x3 - 21x4 = 0
2, 3 и 4 уравнения все одинаковые, от них можно оставить одно.
{ x1 + 4x2 - 7x3 + 13x4 = 0
{ 0x1 - 7x2 + 11x3 - 21x4 = 0
Переменные x3 и x4 - свободные, могут быть какими угодно.
x2 = 11/7*x3 - 3x4
x1 = 7x3 - 13x4 - 4x2 = 7x3 - 13x4 - 44/7*x3 + 12x4 = 5/7*x3 - x4
Это общее решение системы.
Ненулевое решение: например, x3 = 7, x4 = 1, x2 = 8, x1 = 4
{ x1 + 4x2 - 7x3 + 13x4 = 0
{ 2x1 + x2 - 3x3 + 5x4 = 0
{ 3x1 - 2x2 + x3 - 3x4 = 0
{ 3x1 + 5x2 - 10x3 + 18x4 = 0
Умножаем 1 уравнение на -2 и складываем со 2 уравнением.
Умножаем 1 уравнение на -3 и складываем с 3 уравнением.
Умножаем 4 уравнение на -1 и складываем с 3 уравнением.
{ x1 + 4x2 - 7x3 + 13x4 = 0
{ 0x1 - 7x2 + 11x3 - 21x4 = 0
{ 0x1 - 14x2 + 22x3 - 42x4 = 0
{ 0x1 - 7x2 + 11x3 - 21x4 = 0
2, 3 и 4 уравнения все одинаковые, от них можно оставить одно.
{ x1 + 4x2 - 7x3 + 13x4 = 0
{ 0x1 - 7x2 + 11x3 - 21x4 = 0
Переменные x3 и x4 - свободные, могут быть какими угодно.
x2 = 11/7*x3 - 3x4
x1 = 7x3 - 13x4 - 4x2 = 7x3 - 13x4 - 44/7*x3 + 12x4 = 5/7*x3 - x4
Это общее решение системы.
Ненулевое решение: например, x3 = 7, x4 = 1, x2 = 8, x1 = 4
16
Объяснение:
Пусть наибольший общий делитель равен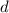 . Тогда числа можно представить в виде
. Тогда числа можно представить в виде 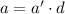 ,
, 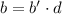 , где
, где 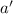 и
и 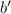 - какие-то натуральные числа.
- какие-то натуральные числа.
У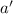 и
и 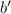 по построению не может быть общих делителей: если бы нашелся общий делитель
по построению не может быть общих делителей: если бы нашелся общий делитель 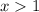 , то существовал бы общий делитель чисел
, то существовал бы общий делитель чисел  и
и 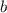 , равный
, равный 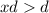 , что противоречило бы тому, что
, что противоречило бы тому, что 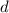 - наибольший общий делитель. Поэтому в
- наибольший общий делитель. Поэтому в 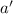 и
и 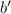 входят все простые делители
входят все простые делители  и
и 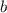 , не являющиеся общими. Получается,
, не являющиеся общими. Получается, 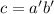
Подставляем всё в равенство из условия и находим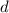 :
: