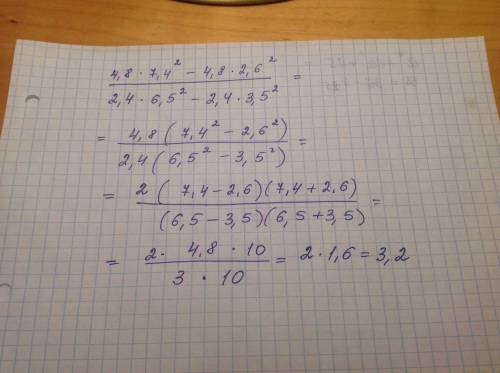
Арифм, прогрессия. Найдите сумму всех двузначных чисел, которые при делении на 4 дают в остатке 3
т.е. число можно представить в виде аn=4n+3. Найдем последний двузначный член прогрессии, т.к. наименьшее трехзначное число равно 100, получим
4n+3<100
4n<97
n<24,25
Т.к. n – целое натуральное число, следовательно, согласно неравенству n<24,25, последний двузначный член имеет номер 24, найдем номер первого двузначного числа
4n+3≥10
4n≥7
n≥1,75
номер первого двузначного числа, , согласно неравенству n≥1,75, первый двузначный член имеет номер 2, найдем необходимые члены прогрессии
а₂=4*2+3=11
а₂₄=4*24+3=99
Сумма n последовательных членов арифметической прогрессии начиная с члена :
Sn=(а₁+аn)*n/2
т.к. надо найти сумму со 2 по 24 член, рассмотрим их как последовательность с 1 по 23 члены, получим
S₂₃=(11+99)*23/2=1265
Удачи!