Алгебра: Решите неравенство а)х²+х-6≤0 б) t²≥3t

Решите неравенство а)х²+х-6≤0 б) t²≥3t

👇

Ответ:

MoonLoveYou

26.04.2021

$1)\; \; x^2+x-6\leq 0\\\\x_1=-3\; ,\; x_2=2\; \; (teorema\; Vieta)\\\\(x+3)(x-2)\leq 0\\\\Znaki:\; \; +++[-3\, ]---[\, 2\, ]+++\\\\x\in [-3,2\, ]\\\\2)\; \; t^2\geq 3t\\\\t^2-3t\geq 0\\\\t(t-3)\geq 0\\\\znaki:\; \; +++[\, 0\, ]---[\, 3\, ]+++\\\\x\in (-\infty ,0\, ]\cup [\, 3,+\infty )$

4,7(74 оценок)

Открыть все ответы

Ответ:

дана399

26.04.2021

Всего в коробке 5 шашек, 2 из которых чёрные и 3 белые.
Наудачу достают две шашки.
Рассмотрим первый вариант, при котором достанут две белые шашки, обозначив его событием А:
Вероятность события А равна: Р(А)=3/5××2/4=6/20=3/10
Рассмотрим второй вариант, при котором достанут две чёрные шашки, обозначив его событием В:
Р(В)=2/5×1/4=2/20=1/10

Вероятность наступления хотя бы одного из двух несовместимых событий равна сумме их вероятностей:
Р (А∪В)=Р(А)+Р(В)=3/10+1/10=4/10=2/5=0,4
ОТВЕТ: вероятность того, что обе эти шашки окажутся одного цвета равна 0,4

4,4(90 оценок)

Ответ:

aleXxxx03

26.04.2021

Объяснение:

Задача №1

Расстояние по течению - 4 км

Расстояние против течения - 3 км

Собственная скорость - х км/час

Скорость течения - 3 км/час

Значит

скорость движения по течению (х+3) км/час

скорость движения против течения ( х-3) км/час

Соответственно время движения по течению 4/(х+3) час.

против течения : 3/(х-3) час

По условию , на путь по течению потрачено на 4 мин. меньше

4 мин.= 4/60= 1/15 часа

Составим уравнение:

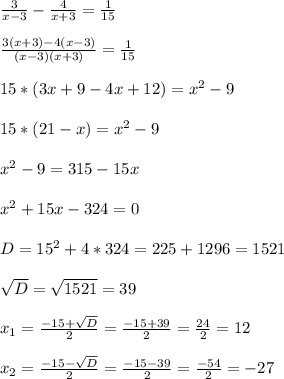
$\frac{3}{x-3} -\frac{4}{x+3}=\frac{1}{15} \\ \\ \frac{3(x+3)-4(x-3)}{(x-3)(x+3) } =\frac{1}{15}\\ \\ 15*(3x+9-4x+12)= x^{2} -9\\ \\ 15*(21-x)= x^{2} -9\\ \\ x^{2} -9=315-15x\\ \\ x^{2} +15x-324=0 \\ \\ D=15^{2} +4*324= 225+1296= 1521\\ \\ \sqrt{D} =\sqrt{1521}=39\\ \\ x_{1} =\frac{-15+\sqrt{D} }{2}= \frac{-15+39}{2}=\frac{24}{2}= 12 \\ \\ x_{2} =\frac{-15-\sqrt{D} }{2}= \frac{-15-39}{2}= \frac{-54}{2}=-27$

Корень х₂= -27 не подходит , поскольку скорость не может быть отрицательной , значит

собственная скорость буксира 12 км/час

Задача №2

Найдем расстояние , которое составили 8/15 пути

225*8/15 = 120 км

Найдем расстояние , которое осталось

225-120=105 км

х км/ч - скорость автомобиля на первом участке пути,

(х-10) км/час - скорость автомобиля на втором участке пути, тогда время, которое потратил автомобиль на 1-й участок пути составит

120/х час, значит на второй участок потратил

105/(х-10) час

Общее время составило 3 часа .

Можем составить уравнение:

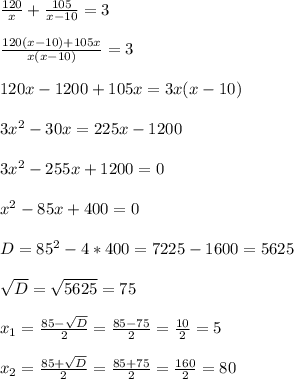
$\frac{120}{x}+ \frac{105}{x-10}= 3 \\ \\ \frac{120(x-10)+ 105x}{x(x-10)}=3\\ \\ 120x-1200+105x=3x(x-10)\\ \\ 3x^{2} -30x=225x-1200\\ \\ 3x^{2} -255x+1200=0\\ \\ x^{2} -85x+400=0 \\ \\ D= 85^{2}-4*400= 7225-1600=5625\\ \\ \sqrt{D}=\sqrt{5625}=75\\ \\ x_{1} =\frac{85-\sqrt{D} }{2}= \frac{85-75}{2}= \frac{10}{2}= 5 \\ \\ x_{2}=\frac{85+\sqrt{D} }{2}=\frac{85+75}{2}=\frac{160}{2}= 80$