Пусть сторона квадрата х см, тогда длина прямоугольника (3х) см, а ширина прямоугольника - (х - 5) см.
Т.к. площадь квадрата находят по формуле S = а², где а - сторона квадрата, о площадь данного квадрата равна (х²) см².
А т.к площадь прямоугольника находят по формуле S = a · b, где a и b - длина и ширина прямоугольника, то площадь данного прямоугольника будет равна S = 3х · (х - 5) = 3х² - 15х (см²).
Т.к. площадь квадрата на 50 см² меньше площади прямоугольника, то составим и решим уравнение:
3x² - 15х = x² + 50,
3x² - x² - 15x - 50 = 0,
2x² - 15x - 50 = 0,
D = (-15)² - 4 · 2 · (-50) = 225 + 400 = 625 ; √625 = 25,
x₁ = (15 + 25)/(2 · 2) = 40/4 = 10,
x₂ = (15 - 25)/(2 · 2) = -10·/4 = -2,5 - не подходит по условию задачи.
Значит, сторона квадрата равна 10 см.
ответ: 10 см.
Это степенная функция с показателем степени равным 0,5 и смещение по оси у на 3.
Плюс здесь есть разница в области определения функции.
найдем ее:
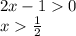
Это область определения.
График можно построить или по точками, или по следующим правилам:
Прибавление некоторой константы эквивалентно сдвигу по оси Оу, например:
если y=f(x)+C, то график этой функции будет выглядеть так же как и график функции y=f(x) , только он будет выше на оси Оу на С единиц.
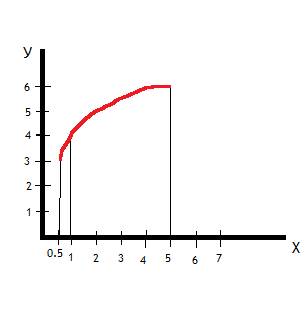
Если строить по точкам то можно воспользоваться следующей таблицей:
Х | 0.5 | 1 | 5
У | 3 | 4 | 6
График можно посмотреть во вложении:
P.S. извиняюсь за качество
(Квадрат действительного выражения ВСЕГДА НЕОТРИЦАТЕЛЕН)
Итого после цепочки равносильных неравенств мы пришли к верному неравенству, значит и исходное неравенство верно.
Доказано