8
Объяснение:
Сложим два равенства, получим уравнение:
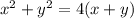
Раскроем скобки справа, перенесем влево и дополним до полных квадратов относительно х и у:
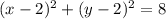
Выражаем x через y:

(вообще, правильнее было бы рассмотреть два случая: когда перед корнем стоит знак плюс, что мы и делаем, и когда перед ним стоит знак минус, но нас интересует максимальное значение, логичнее было бы рассмотреть только положительное значение)
Наша целевая функция, в которой будем находить максимум, имеет вид:
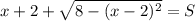 , где S - сумма решений системы уравнений.
, где S - сумма решений системы уравнений.
Найдем производную по х, приравняем к нулю эту функцию
Получим

Таким образом, мы сможем найти y: y₁ = 4; y₂ = 4
Стало быть, только в точке (4;4) достигается этот максимум суммы, которая равна 4+4 = 8
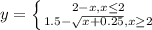
Объяснение:
Рассмотрим случай x ≤ 0
Тогда функция принимает значение

Попробуем выразить явно функцию. Для этого выделим полный квадрат в правой части:
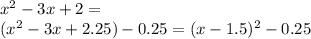
Теперь,

Для x ≤ 0 соответствует корень, взятый с отрицательным знаком. Поэтому обратная функция (просто в полученной функции меняем местами x и y), получим:
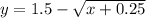 .
.
Т.к. y ≤ 0, найдем соответствующее значение x:
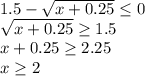
Один кусочек нашли, займемся другим
При x ≥ 0 у нас функция принимает значение:
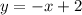
Выразим x через y, и после этого поменяем их местами

Т.е.
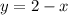
Поскольку y ≥ 0, найдем x, соответствующий этой обратной функции
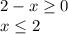
Соединяя все воедино, получим следующую кусочно-заданную функцию:
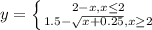
2x - 8 >= 0; x>= 4
6x + 13 >= 0; x >= -13/6
оставим только x >= 4, ибо оно является сильнейшим
теперь можем забить на корень и перейти к уравнению следствию:
2x - 8 <= 6x + 13; корень это возрастающая функция и мы вправе это сделать
4x + 21 >=0
4x >= -21
x>= -21/4
учитывая одз, получаем, что x >= 4