y = f(x)
Сначала осознаем как должен выглядеть график (рис. 1):
Рисуем прямые x = -5 и x = 6, график не должен выходить за эти прямые (обозначили область определения).Рисуем прямые y = -4 и y = 3, график не должен выходить за эти прямые (обозначили множество значений).На оси Ox отмечаем интервал (1;4), график функции должен проходить через ось Ox в этом интервале (обозначили промежуток нулевого значения).Теперь построим график функции (рис. 2):
Для простоты построим график ломанной (она непрерывна и просто изображается).
Функция убывает на всей области определения, поэтому для самого меньшего х из области определения , должно быть самое наибольшее y из множества значений (потом это значение уже не реализуется т.к. функция убывает, тогда множество значений будет другим). Итог: вершина ломанной в точке (-5;3).Пусть следующая вершина в точке (0;2).Ноль функции, он же пусть будет и вершиной ломанной, в точке (3;0) т.к. 3 ∈ (1;4).Последняя вершина в точке (6;-4), y= -4 для нужного множества значений.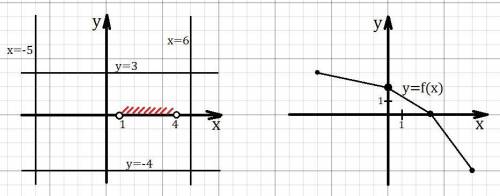
Объяснение:
Пусть имеется некоторый реальный эксперимент и пусть через {\displaystyle {A}}{A} обозначен наблюдаемый в рамках этого эксперимента результат. Пусть произведено {\displaystyle n}n экспериментов, в которых результат {\displaystyle {A}}{A} может реализоваться или нет. И пусть {\displaystyle k}k — это число реализаций наблюдаемого результата {\displaystyle {A}}{A} в {\displaystyle n}n произведённых испытаниях, считая что произведённые испытания являются независимыми.
Числовая функция: {\displaystyle \mathrm {N} _{n}(k)={\frac {k}{n}}\Leftrightarrow {\frac {k(A,n)}{n}}}\mathrm{N} _{n}(k)={\frac {k}{n}}\Leftrightarrow {\frac {k(A,n)}{n}} называется функцией относительной частоты реализаций наблюдаемого результата {\displaystyle {A}}{A} в {\displaystyle n}n независимых реальных экспериментах. Вероятность вычисляют до опыта, а относительную частоту - после опыта.
x²-(x-2)²=16
x²-(x²-4x+4)=16
x²-x²+4x-4=16
4x=20
x=5.
ответ: сторона земельного участка 5 м.