Пусть скорость катера в стоячей воде х км/ч. А по условию задачи скорость реки 2 км/ч. Тогда скорость катера из пункта А в пункт В составляет 15/6=х-2 (км/ч), а скорость на обратном пути 15/2=х+2 (км/ч). Составим и решим систему уравнений.
15/6=х-2 (1)
15/2=х+2 (2)
решая совместно (1) и (2) получим:
15=6х-12;
15=2х+4 ; далее,упрощая 27=6х (3)
11=2х (4), вычитая (4) из (3),получим 16=4х, откуда х=4 (км/ч)
ответ: собственная скорость катера 4 км/ч
4) Обозначим числа x и y. Имеем систему уравнений:
x+y =8
x-y = 12
Сложим уравнения системы: 2x = 20; x = 10; x=10; y = 8-x = 8 - 10 = -2. Решением системы является пара чисел (10:-2).
Заданные числа 10 и -2, их произведение xy= -2*10 = -20.
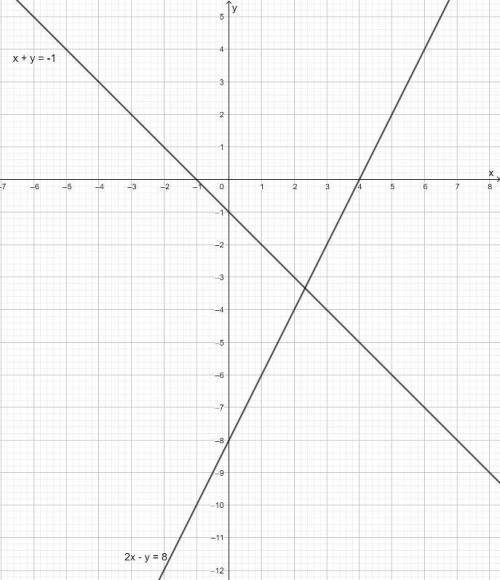
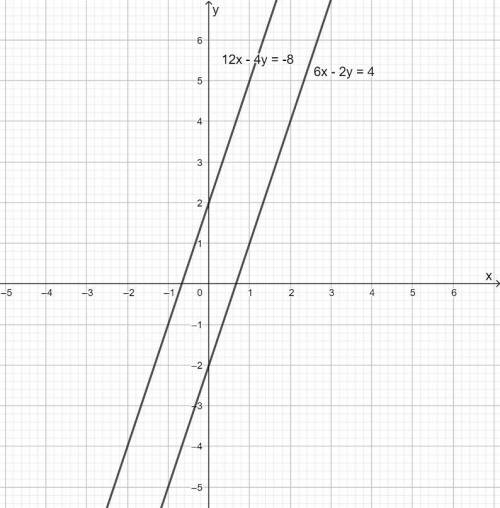
5) Графики во вложении. Система уравнений б) не имеет решений, графики линейных функций параллельны, не имеют общих точек (не пересекаются).
6) Пусть стоимость 1 тетради = x р, 1 карандаша = y р. Стоимость всей покупки 4x + 5y = 2. Имеем линейное уравнение с двумя переменными.
Подставим координаты точек в уравнение линейной функции.
а) 4*0,4 + 5*0,08 = 1,6 + 0,4 = 2 верно
б) 4*0,1 + 5*0,2 = 0,4 + 1 = 1,4 не верно
в) 4*0,35 + 5*0,12 = 1,4 + 0,6 = 2 верно
Пара чисел пункта б) (0,1; 0,2) не является решение задачи.
D= b^2-4ac= (-70)^2-4*1*600=2500, √D=50
x1= (70+50)/2= 120/2 = 60
x2= (70-50/2= 20/2= 10
ответ: 60, 10.